Zad Sophie: Poda mi ktoś jakieś bardzo trudne zadanie z działu liczby rzeczywiste z poziomu rozszerzonego?

Sophie:

Sophie:

Sophie: Ktokolwiek ?

Sophie: kochanus_niepospolitus ?

kochanus_niepospolitus: poszukaj sobie: https://matematykaszkolna.pl/strona/3548.html

Mila: https://www.zadania.info/d1 Tu masz wszystkie działy, z gwiazdkami są trudniejsze.

Sophie: dziękuje za odpowiedz

yht: Pewnego ucznia na lekcji historii zapytano, ile lat trwało panowanie władców polskich: Bolesława Krzywoustego oraz Władysława Jagiełły. Odpowiadając na każde z dwóch pytań, uczeń popełniał błąd bezwzględny, przy czym suma tych błędów wyniosła 16 lat. Wiadomo również, że odpowiedzi ucznia były liczbami naturalnymi, a panowanie Władysława uczeń uznał za 50 % dłuższe od panowania Bolesława. Oblicz błędy bezwzględne i względne popełnione przez ucznia podczas oceny długości panowania obu władców jeżeli wiadomo, że B. Krzywousty panował 36 lat, a W. Jagiełło 48 lat.

klm:

Sophie: wyszło mi bład bezwględny Bolesłąwa Δ=2 a Władysława Δ=14 względne Bolka = 5.5% a Władysława 29,17% ale nie wiem czy dobrze Może ktoś sprawdzić i rozpisać z wyjaśnieniem ? :0

Sophie: Adamm ?

Sophie: Jerzy ?

Adamm: Δ₁+Δ₂=16 Δ₁, Δ₂∊ℤ₊ Δ₁=|36−x|, Δ₂=|48−1,5x| |36−x|+|48−1,5x|=16 1. 36≥x, 48≥1,5x 84−2,5x=16 x=27,2∉ℤ₊, odpada 2. 36<x, 48≥1,5x 12−0,5x=16 x=−8∉ℤ₊, odpada 3. 36≥x, 48<1,5x 0,5x−12=16 x=56 sprzeczność z założeniem 4. 36<x, 48<1,5x 2,5x−84=16 x=40, zgodne z założeniem Δ₁=|36−40|=4 Δ₂=|48−1,5*40|=12

	Δ1		1
δ1=		=
	36		9

	Δ2		1
δ2=		=
	48		4

Sophie: dobrze myślałam tylko nie wiedziałam co zrobić z tym 50%

Sophie: znaczy tego zapomniałam uwzględnić

Sophie: skąd 2,5x

5-latek: Zadanie Wyznacz zbior wszystkich punktow plaszczyzny ktorych wspolrzedne spelniaja rownanie a) |y|x²−2x−3 b) (x+|x|)²+(y+|y|)² =16 Zadanie nr 2 Zapisz w najprostszej formie

√x+y−√x−y		√x+y+√x−y
	+		}
√x+y+√x−y		√x+y−p[x−y

zadanie nr 3 Udowodnij twierdzenie

	a+b
a) dla kazdego ab∊R (a<b⇒a<		<b)
	2

b) dla kazdego a.b ∊R ((a>1 i b<1)⇒ab+1<a+b) Wskazowka do b ) rozloz na czynniki ab−a−b+1 Zadanie nr 4 Udowodnij twierdzenie Dla kazdego ab ∊R (a²+b²≤2⇒|a+b|≤2) Wskazowka 2a²+2b²= (a+b)²+(a−b)²

5-latek: W zadaniu nr 1 jest a) |y|= x²−2x−3 I jeszcze jedno Zadanie nr 5 Zbadaj w zaleznosci od parametru m rozwiazanie nastepujacego ukladu rownan {(m+1)²x+(m²−1)y= m+1 {(m−1)²x+(m²−1)y= (m−1)² Na razie wystarczy Powodzenia

Adamm: zd 1 a) |y|=x²−2x−3, tak ma być? zd 2

√x+y−√x−y		√x+y+√x−y
	+
√x+y+√x−y		√x+y−√x−y

a tu tak?

5-latek: Czesc tak ma byc .

Adamm: Cześć jesteś pewien że to zadania dla Sophie? ona już z równaniami z wartością bezwzględną ma problemy

maciu: A czy wiek kruli ma tu znaczenie.

5-latek: króli

5-latek: Adamm nie wiem W zbiorze zadan Antonowa sa gorsze przyklady do liczenia bo to zbior zadan z 1956r

LWG: Co to jest iloraz rzeczywisty? 'ni '= n/t = n/(nT) = 1/T, trepie, który popireasz zwyrodniaców z Fizyka w Szkole i z FIZYKON. Dopadnę ich na 100%. I CO WÓWCZAS? Nie mam czasu. I tak zdechną.

LWG: Ścierwa zajebali mi odkrycie, że 'ni' = n/t. Za to powinni dostać czapę

5-latek: Posluchaj sobie The Wall PINK FLOYD Tam jest wlasnie o takim Pinku jak Ty . Powinienes znac

5-latek: Zapomnialem dodac O takim PInku co go nikt nie rozumie . jest tez polski przeklad

LWG: No i jak z tym Bealem? Chodzi o Beal Prize. Tylko kontrprzykład? Podać tu trójkę, która spełnia BE (Beal Equation)? Oczywiście A,B, and C are coprime. Taraz nie ma wuja we wsi. Musi być.

LWG: Żartowałem. przecież wiadomo, że to być nie może. Nie? A gdzie na to dowód? Idę po wszystkich, czyli po nikogo. Ale macie szczęście.

LWG: Mogą przyjść po mnie. Jednak w jakim celu? Po prostu po mnie. Ilu szło? kilkunastu. Wszyscy nie żyją. Ale nie zawsze tak jest. Przy czym Ci, którym się to udało − już są u Św. Piotra.

384: rzyciowe

LWG: Krótko. Polscy naukowcy ukradli mi pierwotną definicję częstości obiegów. W ślad za bydlakami poszło ścierwo z FIZYKON. Muszę zwyrodnialców wysłać do Św. Piotra. Tak, czy nie? polscy nakowcy wykradli mi pomysł na funcję podatkową , która zastępuje dowolną liczbę progów podatkowych. Podali inną, ale chyba nie opublikowali odkrycia. Niech więc umrą naturalnie. Ale zablokowali. Zatem dożywocie. A LA KOGO? Nie wiem.Musi być lepiej − dla was.

LWG: 384, doskonale. Co doskonale? Idealny wpis. Treść Twojego wpisu. Ale mnie nie chodzi o ściganie. Daruję im. " PO CO CI TO?" No właśnie. Bardzo się zmęczyłem FE i temu podobnymi. ISBP przebija wszystkie moje wnioski twórcze. Jak chcesz, to zmienię religię.Tego nie uczynię, bo RP nie może należeć do innych. ON WZYWA DO KRADZIEŻY. Chyba ogłoszę się Królem RP. Pogonię wszystkich, oprócz niektórych z PIS. Brednie. Pragnę znakomitego jutra dla każdego Polaka. Opozycja to złodzieje i zdrajcy RP.

5-latek: Tobie tylko jest w stanie teraz pomoc jeden lekarz . Psychiatra .

5-latek: I nie obawiaj sie tego Slawni ludzie a pewnie sie do nich zaliczasz maja swoich prywatnych terapeutow Doranoc .

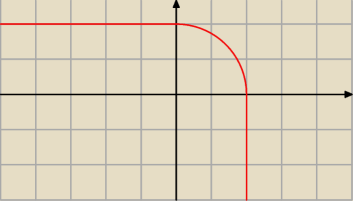
Adamm: Właśnie, myślałem że Sophie pewnie nie zna nawet równania okręgu, więc rozwiąże zd 1 przykład b Inne wydają się na jej obecną wiedzę. (x+|x|)²+(y+|y|)²=16 dla x<0 oraz y<0 mamy 0=16 dla x≥0 oraz y≥0 mamy x²+y²=4, równanie okręgu o promieniu 2 oraz środku (0;0) dla x≥0 oraz y<0 mamy x²=4 x=2 dla x<0 oraz y≥0 mamy analogicznie y=2 Równanie przedstawia nam krzywą na rysunku, w 1 ćwiartce mamy 1/4 okręgu o promieniu 2, w 2 mamy prostą y=2, w 3 nic nie mamy, a w 4 mamy prostą x=2

Sophie: 1 zrobiłam wcześniej ,ale stoje w połowie 2 zadania

Sophie: Milo mogłabyś zerknąć proszę cieplutko

Sophie: mogę to porównać do zera i pomnożyc przez mianowniki ?

Sophie: Saizou ?

Sophie: Piotr ?

Sophie: 3a) mam ,ale podpunkt b) wyszło ab−a−b+1<0 /*(−1) a−ab+b−1<0 (√a−√b)²−1<0 la−bl−1<0 o to chodziło ?

Sophie: ktokolwiek ?

Pytający: Zadanie 2: a=√x+y b=√x−y

a−b		a+b		(a−b)2+(a+b)2
	+		=		=(zastosuj wzory skróconego mnożenia)=
a+b		a−b		(a+b)(a−b)

	2(a2+b2)		2x
=		=(podstaw a, b i uprość)=
	a2−b2		y

Pytający: 3a) Nie o to chodziło. Zauważ, że: ab−a−b+1=a(b−1)−(b−1)=(a−1)(b−1) Co możesz powiedzieć (przy podanych założeniach) o wartości (a−1), a co o wartości (b−1)? I swoją drogą zmieniasz znak nierówności, jeśli mnożysz obie strony nierówności przez liczbę ujemną (tak na przyszłość). Ponadto (√a−√b)²=a−2√ab+b, więc źle zastosowałaś wzór skróconego mnożenia.

Sophie: mógłbyś rozpisać zad 2 te podstawienie cieplutko proszę

Pytający:

	2(a2+b2)		2((√x+y)2+(√x−y)2)
(...)=		=		=
	a2−b2		(√x+y)2−(√x−y)2

	2(x+y+x−y)		4x		2x
=		=		=
	x+y−(x−y)		2y		y

Mroźnie odpowiadam.