Wartosc bezwzgledna 5-latek: Dla s No to w ramach pocwiczenia łap Zadanie nr 1 Rozwiaz rownanie |x+1|−|x|+3|x−1|−2|x−2|= x+2 Zadanie nr 2 Rozwiaz rownanie |y|+y+|x|+x=0 Zadanie nr 3 Rozwiaz uklad rownan {|x−1|+|y−5|= 1 {y=5+|x−1| Wystarczy

s: robie

5-latek: Dobrze

s: wskazówka do 1)

5-latek: Robisz przedzialami . Bedzie ich 5

s: 1) x=6 v x=0

s: 2) 2y+2x=0

5-latek: Wolalbym zeby byly obliczenia Masz zle zadanie nr 1 x=−2 lub x≥2

5-latek: Skoncz najpierw zadanie nr 1 Potem sie zastanow nad zadaniem nr 2 Proponuje pisac zgodnie z definicja watosci bezwzglednej

s: tam we wszystkich przedziałach przy lxl bedzie −x ?

5-latek: Nie Potrafisz ustalic jakie tutaj beda przedzialy?

s: x<1 x∊(−1,0) x∊(0,1) x∊(1,2) x∊(2,∞)

s: i już wszytstko wyliczyłam i nie wychodzi

5-latek: Pierwszy przedzial x<−1 czyli x∊(−∞ −1) teraz jesli ten jest otwarty to drugi domykasz lewostronnie 2) x∊<−1,0) 3) x∊<0,1) 4x∊<1,2) 5x∊<2,∞) Domykasz go dlatego ze np do 1 nie nalezy −1 ale do drugiego juz tak Teraz napisz to rownanie do 1 przedzialu

5-latek: Nikt nie powiedzial ze bedzie latwo zwlaszcza na rozszserzeniu .

s: −x−1−x−3x+1+2x−4=x+2

5-latek: Zle najlepiej rozpisuj sobie moduly x∊(−∞ −1) w tym przedziale |x+1|= −(x+1)= −x−1 |x|= −x |x−1|= −(x−1)= −x+1= 1−x (bo dodawanie jest przemienne ale odejmowanie juz nie |x−2|= −(x−2)= 2−x Teraz −x−1−(−x)+3(1−x)−2(2−x)=x+2 −x−1+x+3−3x−4+2x=x+2 dokoncz i nastepne przedzialy

s: x=−2 ,ale nie x≥2

5-latek: Przeczytaj moje ostanie zdanie z postu 12 : 48 i zastosuj sie do niego czy x=−2 nalezy do tego przedzialu ? Jesli tak to jest rozwiazaniem .

s: dlaczego lxl=−x ?

5-latek: Tak podejrzewalem ze tutaj sa duze klopoty Jakie mamy liczby w przedziale x∊(−∞,−1) dodatnie czy ujemne ? Co wtedy mowi na definicja wartosci bezwzgledej ? Co robimy opuszczajac modul? A tak w ogole to napisz definicje wartosci bezwzglednej.

s: Wartość bezwzględna z liczby dodatniej to ta sama liczba a jak minus to na plus

5-latek: jak jest w module liczba ujemna to zmieniamy znak na przeciwny np |−5|= −(−5)=5 teraz |x|=−x dla x<0 w przedziale (−∞ −1) sa same liczby ujemne Teraz widzisz dlaczego w tym przedziale |x|=−x?

5-latek: Teraz nastepny przedzial

s: robiłam inne zadania 2 przedział to x+1+x−3x+3+2x−4=x+2 0=2 sprzeczne

s: znaczy x=−2

s: A jak będzie wyglądało 2 ?

s: nie mówie ,że robiłam inne tylko patrzyłam na definicje wartocii bezwzglednej

s: 5−latek ?

s: Jerzy zerkniesz?

Jerzy: Rozpatrujesz 4 przypadki w zależności od znaku x i y.

5-latek: Skoncz 1 zadanie Do drugiego zadania Zauwaz ze ⋀x∊R |x|+x≥o Dla kazdego y∊R |y|+y≥0 Teraz |x|+x+|y|+y=0 wtedy i tylko wtedy gdy (|x|+x=0 i |y|+y=0 ) Kiedy to nastapi ? Albo rozpatruj przypadki tak jak napisal Jerzy Czesc .

Jerzy: Witaj

s: i co jak wychodzi 2x+2y =0 w każdym z przedziałów ?

Jerzy: Nie w każdym.

5-latek: Napewno tak nie wychodzi 1. dla x≥0 i y≥0 dostajemy 2x+2y=0 (pomysl przez chwile kiedy to rowna sie 0? Kiedy x= ? i y= ? 2 x≥0 y y<0 masz wtedy x+x−y+y=0 to 2x=0 to x=0 3. x<0 y≥0 masz 2y=0 to y=0 4 x<0 y<0 −x+x−y+y=0 to 0=0 (tozsamosc Wiec kiedy to rownanie =0 ? Dawaj odpowiedz

s: 1)2y+2x>0 0=0 2x=0 2y=0

s: 0

Jerzy: Źle.

Jerzy: 2x + 2y = 0 2x = −2y x = −y

s: w układzie równan podstawiłąm w pierwszym za y i wyszły przedziały x∊(−∞;1/2 ; 3/2;∞) i nie wiem co teraz z drugim

Jerzy: O czym ty bredzisz ?

Jerzy: 1) x = 0 i y = 0

s: Zad 3 Zapomniałam dopisać sorki Jerzy

5-latek: Wroc jeszce do zadania nr 2 Zauwaz ze to rownanie =0 kiedy x=0 i y=0 lub x<0 i y<0 ======================================================== To trzecie zadanie jest tez trudne i nalezy troche nad nim pomyslec Tak jak napisalas/es z drugiego rownania |x−1|= y−5 Wstawiamy do pierszsego rownania y−5+|y−5|=1 Teraz analiza |x−1|=y−5 Wiemy ze wartosc bezwzgledna jest zawsze nieujemna tzn ≥0 wiec z tego masz ze y−5≥0 Teraz |y−5| musi sie rownac y−5 wtedy masz rownanie y−5+y−5=1 2y−10=1 to y=5,5 Teraz |x−1|= y−5 |x−1|= 5,5−5= 0,5 Teraz rozwiaz to rownanie i wyznacz x (beda dwa takie x_sy Zauwaz ze |y−5| tutaj nie moz ebyc rowna 5−y bo wtedy dostaniesz rownanie sprzeczne y−5+5−y=1 to 0=1 sprzecznosc

5-latek: Wiec napisz rozwiaznie zadania nr 3 Potem skoro to ma byc rozszsrzenie to Zadanie nr 4 Rozwiaz nierownosc x²−|x|<0 a) rachunkowo b) graficznie Zadanie nr 5 Naszkicuj wykres funkcji f(x)=y= (1+|x|)(2−|x|) Zadanie nr 6 Sporadz wykres nierownosci |x|−|y|≥1

s: x=1,5 i x=0,5

s: do tego powyżej

ignite: dobrze zrobiłeś

s: 4) x=0 x=1 x=0 x=−1

ignite: ale jest jeszcze jeden x

s: Zrobiłam!

ignite: eee sory zagapiłem się

ignite: przepraszam Panią najmocniej

ignite: tą metodę graficzną to masz trochę dziwną

ignite: nie rozumiem też dlaczego z nierówności wyszły Ci równości

s: ciężko się rysuje proszę Pana

s: x∊(−∞;−1) u (0;1)

ignite: pierwszy przedział źle, drugi ok

ignite: możesz napisać jak do tego doszłaś?

s: (−1;0)

s: zapomniałam zmienic znak ,ale już wszystko ok

s: zaczynam to rozumieć

s: zły wykres ,ale ja nie umiem w tym programie ,ale przedziały są dobrze

s: oczywiście nie te na wykresie

ignite: pewnie to chciałaś narysować

s: Dzięki proszę Pana

ignite: Rysujesz zad. 5?

s: próbuje i średnio

s: x∊(1;∞) ,ale wątpie sprawdzi ktoś ?

ignite: a uczyłaś się już o funkcji kwadratowej?

s: nie bedzie fkwadratowej

ignite: dziedziną są liczby rzeczywiste

s: jak ?

ignite: nie masz żadnego pierwiastka, ani dzielenia w funkcji

s: Jerzy możesz spojrzeć ?

ignite: najpierw musisz podziałać na przedziałach y = (1+|x|)(2−|x|) w moduły( |x| ) masz takie same czyli przedziały także więc: x∊(−∞,0) −> y = (1−x)(2+x) x∊<0,∞) −> y = (1+x)(2−x) no i obliczasz sobie dla poszczególnych przedziałach, rozumiesz?

s: tak ,dzięki

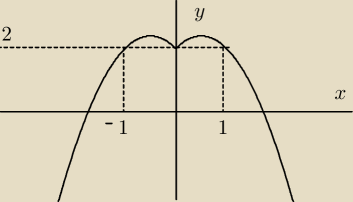
ignite: Wyszło tak?

s: to będą trzy przedziały w sumie

s: x∊(−∞;−2) u (1;∞) u (−√2; √2 )

s: czyli mam źle

ignite: przedziały masz 2, te co Ci napisałem

s: no tak ,ale z pierwszego wychodzą dwa bo mniejsze od 0

ignite: no teraz to mnie troszkę zakłopotałaś o.O

s: wiec kto ma dobrze

ignite: no masz źle nie może Ci z jednej wartości bezwzględnej wyjść 3 przedziały

s: ale to jest całość cześć wspolna obu

s: wartośći bezwzględnych

s: spjrzy ktoś

ignite: zaraz Ci napisze jak ogólnie się zadania z wartością bezwzględną, bo nadal tego nie rozumiesz

ignite: Popatrz kiedy masz dowolną równość lub nierówność musisz zacząć od wyznaczenia miejsc zerowych w wartości bezwzględnej np. : |x−3|+|x−2|+|x+5|−|x|=20 Tych modułów(wartości bezwzględnych) masz 4, więc rozpatrujesz równanie dla 5 przedziałów po obliczeniu ich miejsc zerowych. x−3=0 => x=3 x−2=0 => x=2 x+5=0 => x=−5 x=0 Z tego budujesz przedziały, rosnąco miejscami zerowymi, a od drugiego przedziału są one lewostronnie domknięte: (−∞,−5) <−5,0) <0,2) <2,3) <3,∞) Teraz na podstawie tych przedziałów podstawiasz dowolną liczbę z tego przedziału i sprawdzasz czy wartość bezwzględna jest ujemna czy nieujemna czyli dla przykładu: (−∞,−5) weźmiemy −6, |x−3| => |−6−3|=|−9|=13 więc zamiast |x−3|, piszesz −(x−3)=3−x bo wartość była ujemna, w przypadku gdyby była nieujemna nie zmieniamy modułu itd. Po takiej operacji nasze równanie przyjmuje postać: 3−x−x+2−x−5+x=20 Łatwo wyliczamy, że: x=−10 Następnie sprawdzamy, czy należy do badanej dziedziny, jak widać należy, a czynność powtarzasz dla wszystkich przedziałów. W przypadku kiedy wyjdzie Ci coś takiego: 0=0 to wynikiem jest cały badany przedział, a kiedy np. 2=3 to nie ma rozwiązania dla przedziału.

ignite: Możesz sobie tą funkcje przekształcić do postaci ogólnej wtedy: y = (1+|x|)(2−|x|) = = 2−|x|+2|x|−|x|² = = −|x|²+|x|+2 Mam nadzieję, że teraz widzisz że trzeba zbudować 2 przedziały

s: x=2 i x=−2

ignite: to są miejsca zerowe tej funkcji

s: wiem x∊(−∞;−2) u (2;∞)

ignite: do której klasy chodzisz?

s: czyli źle?

ignite: tzn. twoim zadaniem było narysowanie funkcji a nie obliczanie dla jakich przedziałów funkcje przyjmuje wartość poniżej zera

s: ale na podstawie monotonicznosci rysuje wykresy

ignite: no dobra ale co to jest x∊(−∞;−2) u (2;∞)?

s: no to już wcześniej narysowałam wykres ,chyba muszę odpoczać i jeszcze raz przestudiować

s: A ty do której ?

ignite: aktualnie 2 technikum

ignite: prześpij się z tym jutro sobie to zrobisz na spokojnie

Sophie:

Sophie: znacie jakieś strony gdzie są podobne zadania ?

Sophie: kochanus_niepospolitus ?

Sophie: ktokolwiek ?

yht: zadania z wartości bezwzględnej z odpowiedziami: https://www.sendspace.com/file/rczp33

Jack: https://www.zadania.info/d181

Jerzy: Rozwiąż takie: |x − 4| = −2

Sophie: nie ma rozwiazn

Sophie:

Sophie:

Adamm: a uzasadnienie?

Sophie: x>0 x=2 l2−4l≠−2 x<0 x=−2 l−2−2l≠−2

Adamm:

Sophie: Wartość bezwzględna liczby ujemnej, jest równa jej liczbie przeciwnej.

Sophie: to jak to napisać Adamm ?

Adamm: twoim sposobem by było tak 1. x−4≥0 ⇔ x≥4 x−4=−2 x=2 ale zgodnie z założeniem, x≥4, sprzeczność 2. x−4<0 ⇔ x<4 4−x=−2 x=6 ale zgodnie z założeniem x<4 ale łatwiej jest tak wartość bezwzględna jest zawsze ≥0 więc od razu widać że równanie jest sprzeczne

Sophie: dzięki

kryst12: rozwiaz rachunkowo i graficznie uklad rownan: {3x−y−1=0 i =6x+2y−4=0

6latek: Masz nastepujace metody rozwiazan algebraicznych ukladu rownan a) przez podstawienie 2) metoda przeiwnych wspolczynnikow 3) metoda wyznacznikowa Wszystkie te metody miales pewnie omawiane na lekcji .Wiec dzialaj Graficzne Postac ogolna prostej przeksztalc do postaci kierunkowej i rysuj wykres jednej i drugiej