trapez Y: Pokaż że nie istnieje trapez spełniający podane niżej warunki: a) różnica długości jego ramion i jego boków jest jednakowa i wynosi 2 b) różnica kwadratów długości jego ramion wynosi 28

Jerzy: a) Niech: a,b − podstawy ; c,d − ramiona Warunek: (a − b)² > |c² − d²| a − b = 2 c − d = 2 ⇔ c = d + 2 4 > |(d + 2)² − d² ⇔ 4 > 4d + 4 ⇔ 1 > d + 1 ⇔ d < 0

Jerzy: b) istnieje.

Blee: a) można wykazać pokazując nie spełnienie nierówności trojkata b) oczywiście że istnieje. Różnica długości podstaw w takim trapezie będzie wynosić √28 = 2√7

Y: Muszę uściślić.Spełnione powinny być jednocześnie oba warunki.To chyba czytelne! Czyli koniunkcja tych warunków a nie alternatywa

Jerzy: To nie wymieniaj w podpunktach a) i b) , bo to sugeruje dwa przypadki !

Jerzy: Kiedy koniunkcja jest prawdziwa ?"

Y: No ale zadanie i tak rozwiązane[ Jerzy d=0 ]

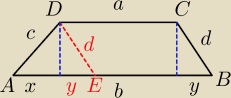
an: b−a=2 c−d=2 c²−d²=28 ⇒ c=8 d=6 AE=x+y=b−a=2 rozpatrzmy istnienie ΔADE AE=x+y=b−a=2 c=d+x+y 8=6+2 ⇒ΔADE ma h=0 Czyli nie ma trapezu o podanych zależnościach boków