Zadanie nana:

	sin6x
lim =(		)
	8x

x→0 =3/4

Jerzy: sin6x/6x*6x/8x

nana:

	(sin6x)'*8x−sin6x*(8x)'		6cosx*8x−sin6x*8*1
=		=		=teraz podstawić 0
	(8x)2		8x2

	(6*1*8*0)−6*0*8*1		0
		=
	(8*0)2		0

nana: Jerzy co robię nie tak

Adamm:

	sin6x
po co ci pochodna z		?
	8x

nana: po podstawieniu 0 jest 0/0 wiec hospital jak nie to juz nie wiem jak byś mógł napisać

Jerzy:

	6		3
= 1*		=
	8		4

Jerzy:

	sin6x
lim		= 1
	6x

nana: no tak na początku napisałam 3/4 to było ok

Jerzy: Popatrz18:50

Jerzy: Teraz widzisz ?

nana: widze i bo juz nie wiem

nana:

	sin6x
=		*{6x}{8x}
	6x

nana:

sin6x		6x
	*		ale jak to zrobiłeś
6x		8x

Jerzy:

	6		3
sin6x/8x = sin6x/6x * 6x/8x...i granica = 1*		=
	8		4

Benny: 19:18 Tak się nie liczy z de l'Hospitala

Adamm:

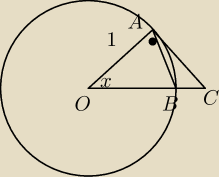
	sinx
granica		→1 przy x→0 jest elementarna, a dowodzi się ją geometrycznie
	x

kąt OAC jest prosty okrąg jest jednostkowy

	1
PΔAOB=		sinx
	2

	1
Płuk AOB=		x
	2

	1
POAC=		tgx
	2

więc zachodzą nierówności sinx<x<tgx dla x będącego kątem ostrym, x∊(0;π/2)

	sinx		sinx
skąd cosx<		<1 a korzystając z tego że cosx oraz		są parzyste,
	x		x

nierówność zachodzi dla x∊(−π/2;0)∪(0;π/2)

	sinx
i teraz z tw. o 3 ciągach mamy przy x→0,		→1
	x