Otoczka wypukła Mariusz: http://wazniak.mimuw.edu.pl/index.php?title=Zaawansowane_algorytmy_i_struktury_danych/Wyk%C5%82ad_11 Tutaj jest przedstawiony pseudokod przetłumaczony z książki Cormena, Rivesta, Leisersona i Steina Jeśli chodzi o punkt pierwszy to najpierw szukać minimum ze względu na współrzędną y a następnie wśród punktów o najmniejszej współrzędnej y znaleźć minimum ze względu na współrzędną x Punkty przechowywać na liście czy w tablicy ? Co do sortowania to tablice można posortować kopcem a listę przez scalanie Jak usuwać elementy aby nie zwiększyć sobie złożoności ? Dodać pole ze zmienną logiczną do rekordu czy jakoś inaczej Przydałoby się też przeliczyć te współrzędne biegunowe względem p₀ Jak zrealizować ten warunek dla pętli while w kroku 9.

Pytający: Od razu szukasz minimum ze względu na y (i na x, jeśli y są równe): min=p0 for(p=p1...pn) if(p.y<min.y || (p.y==min.y && p.x<min.x)) min=p Możesz przechowywać w tablicy. W powyższym szukaniu minimum posługujesz się indeksami i na koniec wrzucasz minimum na pierwszą pozycję w tablicy. Następnie możesz posortować (np. kopcowaniem, żeby było O(nlog(n))) pozostały fragment tablicy (1..n). Jako wartość, wg której porównujesz (sortujesz) punkty p_a i p_b możesz użyć iloczynu wektorowego p₀p_a x p₀p_b. Ach, i wcale nie musisz usuwać punktów współliniowych o mniejszej odległości od p₀. Wtedy należy w drugiej kolejności posortować wg rosnącej odległości. Te funkcje chyba wyglądałyby tak (mogłem pomylić znaki, nie uruchamiałem/testowałem, taki pseudokod): // cross product p0p1 x p0p2 float direction(point p0, point p1, point p2) { return (p1.x−p0.x)*(p2.y−p0.y)−(p2.x−p0.x)*(p1.y−p0.y); } float distSquared(point a, point b) { return (a.x−b.x)*(a.x−b.x)+(a.y−b.y)*(a.y−b.y); } // returns true for a<b, false otherwise bool comp(point p0, point a, point b) { float d=direction(p0,a,b); return d ? d>0 : distSquared(p0,a)<distSquared(p0,b); } Do sprawdzenia tego warunku z kroku 9 wykorzystujesz właśnie iloczyn wektorowy. Przechodząc przez punkty p_a, p_b, p_c (odcinki p_ap_b i p_bp_c) w punkcie p_b: − skręcasz w lewo, jeśli direction(p_a,p_b,p_c)>0 − skręcasz w prawo, jeśli direction(p_a,p_b,p_c)<0 − lecisz prosto (w tym samym kierunku, może być do tyłu (acz nie po posortowaniu jak w tym algorytmie)), jeśli direction(p_a,p_b,p_c)==0

Pytający: Tylko bez usunięcia punktów o tej samej współrzędnej polarnej warunek z punktu 9 musisz zamienić na "punkt p_i nie jest na lewo od wektora (...)".

Mariusz: W rekordzie reprezentującym punkt trzymać tylko współrzędne kartezjańskie czy zarówno kartezjańskie jak i biegunowe Co do sortowania to można wykorzystać ten kod https://matematykaszkolna.pl/forum/333816.html Stos też proponujesz zrealizować na tablicy ?

Mariusz: Znalazłem w sieci pewien kod http://files.derynski.net/moje_prace/graham.c i ciekaw jestem jak go uprościć czy zmienić tak aby kod ładniej wyglądał poza tym użyty algorytm nie gwarantuje złożoności O(nlogn) a algorytm ma być szybszy niż algorytm Jarvisa

Pytający: Cóż, polecam "nie wyważać otwartych drzwi", czyli nie pisać jeszcze raz sortowania czy wyszukiwania minimum. A jeśli chcesz to zrobić tak dla poćwiczenia, to napisz całość samemu od początku do końca, a nie przerabiaj czyjś kod. Toteż jeśli pisałbyś w cpp polecam: http://en.cppreference.com/w/cpp/algorithm Zamiast tablicy, użyj std::vector. Wtedy przykładowo sortowanie sprowadza się do jednej linijki: std::sort(v.begin()+1, v.end(), comp); Zdaje się, że takie coś działa: https://ideone.com/HENzFB Acz wypadałoby dorzucić sprawdzanie ilości punktów na początku. I ta funkcja zmienia przekazany wektor punktów, więc jeśli tego nie chcesz należałoby działać na kopii punktów.

Mariusz: Pytający z tym iloczynem wektorowym to byłbym jednak ostrożny 1. Iloczyn wektorowy jest wektorem 2. Działa dla wektorów w przestrzeni trójwymiarowej 3. Wprawdzie długość tego wektora można powiązać z sinusem ale potrzebowalibyśmy pierwiastka którego chcemy uniknąć inaczej równie dobrze moglibyśmy użyć czteroćwiartkowego arcusa tangensa W C jest on nazwany atan2(y,x) Przeskalowaną wartość cosiniusa można znaleźć z iloczynu skalarnego a przeskalowaną wartość sinusa można znaleźć porównując dwa wzory na pole trójkąta (jeden z wyznacznikiem a drugi z sinusem) Cosinus mógłby być dobry do porównywania kątów ale tylko w przedziałach <0°,180°> oraz <180°,360°> a nie na całym przedziale <0°,360°> ponieważ jest malejący gdy sinus >0 a rosnący gdy sinus < 0

Mariusz: Coś więcej o sortowaniu według więcej niż jednego pola ?

Pytający: Co do sortowania: sortujesz wg pierwszego pola. Jeśli wartości są równe, sortujesz wg drugiego pola, itd. (w zależności od ilości pól, wg których sortujesz). Przykładowo jeśli sortujesz wg nazwiska i imienia, imiona porównujesz jedynie w przypadku takich samych nazwisk. Co do iloczynu wektorowego: to bądź ostrożny. Tutaj używamy go jedynie do określenia wzajemnego położenia 3 punktów. Określamy, w którą stronę skręcamy przechodząc kolejno przez punkty p_a, p_, p_c, o czym wyżej pisałem. Interesuje nas tylko informacja o skręcie (lewo/prawo/prosto). Stąd żadne pierwiastki czy arcusy nie są tu potrzebne. Swoją drogą napisana tu: https://ideone.com/HENzFB przeze mnie metoda direction(p0,p1,p2) zwraca dokładnie to samo, co otrzymalibyśmy obliczając wyznacznik det(p0,p1,p2) z Twojego pierwszego linku w tym wątku: http://wazniak.mimuw.edu.pl/index.php?title=Zaawansowane_algorytmy_i_struktury_danych/Wyk%C5%82ad_11 Zatem, jeśli podejście z iloczynem wektorowym Ci nie leży, skorzystaj z takowego wyznacznika − rezultat ten sam.

Mariusz: Co do sortowania to dotychczas sortowałem tylko według jednego pola kluczowego struct Point { int x,y; }; void Przesiewanie(int l,r, struct Point * A) { struct Point p=A[l]; int i=l; int j=2*i; int isHeap=0; while( j<=r && !isHeap) { if(j<r && A[j].y<A[j+1].y) j++; if(p.y<A[j].y) { A[i]=A[j]; i=j; j=2*i; } else isHeap=1; } A[i]=p; } void BudujStog(int n,struct Point *A) { int i; for(i=n/2;i>=1;i−−) Przesiewanie(i,n,A); } void SortowanieStogowe(int n,struct Point *A) { struct Point p; int i; BudujStog(n,A); for(i=n;i>=2;i−−) { p=A[1]; A[1]=A[i]; A[i]=p; Przesiewanie(1,i−1,A); } } Sortuje punkty według rzędnej Jak zmodyfikować kod aby w drugiej kolejności sortował punkty według odciętej ? Czy modyfikacja taka nie zwiększy asymptycznej złożoności kodu Tutaj na ważniaku chyba niezbyt poprawnie przetłumaczyli pseudokod Cormena U Cormena jest "...sorted by polar angle in counterclockwise order around p0... Counterclockwise to przeciwnie do ruchu wskazówek zegara czyli rosnąco Reszta wygląda na dobrze przetłumaczone Ma to znaczenie czy sortujemy rosnąco czy malejąco Napisałeś "Jako wartość, wg której porównujesz (sortujesz) punkty pa i pb możesz użyć iloczynu wektorowego p0pa x p0pb." Pisałem o tych wartościach sinusów i cosinusów i o przedziałach w których są rosnące jakbym chciał względem ich wartości sortować zamiast względem miary kąta a cała zabawa z tym sinusem ma chyba jedynie porównać miary dwóch kątów tzw stwierdzić który z dwóch kątów ma mniejszą(większą) miarę lub czy są równe Twoja funkcja wystarczy do porównywania kątów ? Gdyby funkcja zwracała wartości takie jak np znana z C funkcja strcmp to można by stwierdzić czy miara kąta jaki tworzy odcinek ap0 z osią biegunową jest mniejszy, większy bądź równy mierze kąta jaki tworzy odcinek bp0 z osią biegunową Jeżeli chodzi o "iloczyn wektorowy" to zdaje się że piszemy o tym samym tyle że nazwa której używasz jest według mnie niepoprawna

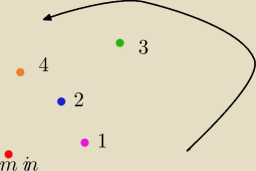
Pytający: Porównując punkty a, b jedynie wg współrzędnej y, punkt a jest "mniejszy" od punku b (wg sortowania), gdy: a.y<b.y Jeśli chcesz porównywać w drugiej kolejności wg współrzędnej x, punkt a jest "mniejszy" od punku b (wg sortowania), gdy: a.y<b.y || (a.y==b.y && a.x<b.x) Toteż trzeba jedynie zmodyfikować porównywanie elementów, w jakikolwiek sposób byś nie sortował. Złożoność asymptotyczna oczywiście się nie zmienia. W najgorszym przypadku wszystkie porównywane pola wszystkich elementów są równe, więc algorytm działałby m razy dłużej, gdzie m to liczba pól, wg których porównujemy elementy, czyli stała niezależna od rozmiaru danych wejściowych. Oczywiście to sortowanie przez kopcowanie wrzucone przez Ciebie wyżej to tylko przykład? Bo w tym algorytmie (Grahama) nie musisz sortować punktów po współrzędnych. Musisz jedynie znaleźć punkt minimalny (w czasie liniowym), a następnie posortować pozostałe punkty wg położenia (polarnego) względem tegoż minimalnego punktu. Co do tego, czy posortujemy te punkty malejąco/rosnąco: to (prawie) nie ma znaczenia, o ile będziemy mieli na uwadze, jak je posortowaliśmy i odpowiednio zmydyfikujemy dalszą część algorytmu (zamiast sprawdzać, czy mamy skręt w prawo, trzebaby sprawdzić, czy mamy skręt w lewo itp.). W wyniku różnica będzie jedynie w kolejności punktów na otoczce (clockwise/countercloskwise). Z tego co się orientuję, w grafice raczej jest preferowany kierunek countercloskwise, więc lepiej posortować tak, jak zaznaczyłem na rysunku (bo malejąco/rosnąco też niekoniecznie jest jednoznacznym stwierdzeniem − wszystko kwestia konwencji). I tak, ta "moja" funkcja zupełnie wystarczy do sortowania, znowuż patrz rysunek, przykładowo: − porównujemy punkty ● i ●: przechodząc ●→●→● skręcamy w lewo ⇒ ●<● (w sensie kąta) − porównujemy punkty ● i ●: przechodząc ●→●→● skręcamy w prawo ⇒ ●>● (w sensie kąta) − porównujemy punkty ● i ●: przechodząc ●→●→● nie skręcamy (wsteczny ) ⇒ trzeba porównać odległości od ● ⇒ ●>● (w sensie kąta, a w drugiej kolejności odległości od min) I zgadzam się, na pewno niekoniecznie poprawnie używam niektórych nazw.

Mariusz: Oprócz tego co na ważniaku to widziałem jeszcze /* Pseudokod algorytmu Grahama znaleziony w książce CLRS Introduction to algorithms Third Edition */ GRAHAM−SCAN(Q) 1 let p0 be the point in Q with the minimum y−coordinate, or the leftmost such point in case of a tie 2 let <p1,p2,…,pm> be the remaining points in Q, sorted by polar angle in counterclockwise order around p0 (if more than one such point has the same angle, remove all but the one that if farthest from p0) 3 let S be an empty stack 4 PUSH(p0,S) 5 PUSH(p1,S) 6 PUSH(p2,S) 7 for i=3 to m 8 while the angle formed by points NEXT−TO−TOP(S), TOP(S), and pi makes a nonleft turn 9 POP(S) 10 PUSH(pi,S) 11 return S /* Funkcja wzięta z książki Sedgewicka napisanej w czasach gdy przykłady dawał w języku C */ int ccw(struct point p0, struct point p1, struct point p2) { int dx1,dx2,dy1,dy2; dx1 = p1.x – p0.x; dy1 = p1.y – p0.y; dx2 = p2.x – p0.x; dy1 = p2.y – p0.y; if (dx1*dy2 > dy1*dx2) return 1; if (dx1*dy2 < dy1*dx2) return −1; if ((dx1*dx2 < 0) | | (dy1*dy2)) return −1; if ((dx1*dx1+dy1*dy1) < (dx2*dx2+dy2*dy2)) return 1; return 0; } /* Co do funkcji Sedgewicka mam wątpliwości bo gdy sprawdzałem jego funkcję do algorytmu Jarvisa to zatrzymywał dając błędne wyniki */ /* Poprawiony kod sortowania stogowego przedstawionego przez Bennego Benny tak skonstruował pętle w funkcji przesiewającej że gdy iteracja nie zmieniała wartości zmiennej j otrzymywał nieskończoną pętle */ /* Funkcja przywracająca własność kopca przy założeniu że tylko węzeł l zaburza własność kopca o rozmiarze p */ void Przesiewanie(int l,int p, int *A) { int x; int i,j; int czyStog; x=A[l]; i=l; j=2*i; czyStog=0; while( j<=p && !czyStog) { if(j<p && A[j]<A[j+1]) j++; if(x<A[j]) { A[i]=A[j]; i=j; j=2*i; } else czyStog=1; } A[i]=x; } /* Funkcja budująca kopiec o rozmiarze n */ void BudujStog(int n,int *A) { int i; for(i=n/2;i>=1;i−−) Przesiewanie(i,n,A); } /* Sortuje n elementową tablicę przez kopcowanie */ void SortowanieStogowe(int n,int *A) { int x; int i; BudujStog(n,A) for(i=n;i>=2;i−−) { x=A[1]; A[1]=A[i]; A[i]=x; Przesiewanie(1,i−1,A); } } Co do stosu to na upartego można go zrealizować na tablicy Chociaż według mnie wygodniej byłoby zrealizować go na liście struct point{ int x,y; }; W implementacji tablicowej mamy dwie zmienne całkowite int stackSize=0, top=−1; Stos jest pusty gdy top==−1; Stos jest przepełniony gdy top>=stackSize; Tablica przechowująca elementy stosu struct point *stack; Alokacja pamięci na stos stack=( struct point *)malloc(stackSize*sizeof(struct point)); Zwalnianie pamięci na stos free(stack) Wierzchołek stosu stack[top]; Element pod wierzchołkiem stosu stack[top−1] Odkładanie wartości na stos struct point p; top++; stack[top]=p; Usuwanie elementu ze stosu top−−; Czy funkcja znaleziona u Sedgewicka nadaje się do porównywania kątów i sprawdzania warunku z punktu 8 Jeśli tak to w jaki sposób Dlaczego dla tablic chciałbym użyć sortowania przez kopcowanie − nie zwolni do O(n²) jak sortowanie przez podział − nie wymaga dodatkowej pamięci O(n) jak sortowanie przez scalanie Co otrzymamy gdy w funkcji przesiewającącej operator porównania zastosowany do elementów tablicy zastąpimy twoją funkcją ? Czy funkcja sortująca przez kopcowanie będzie wtedy sortowała poprawnie ? Tak na dobrą sprawę to największy problem sprawia punkt 2 tego pseudokodu bo po przeczytaniu tego co na ważniaku warunek z punktu 8 można stosunkowo łatwo zrealizować pisząc odpowiednią funkcję Mimo iż z punktem 1 jakoś bym sobie poradził to pokazałeś mi jak go lepiej zrealizować Ze stosem raczej nie miałbym problemów zarówno z tym na liście jak i z tym na tablicy Warunek z punktu 8 można stosunkowo łatwo zrealizować po przeczytaniu tego co na ważniaku Zostaje więc punkt 2 który podobno zajmuje najwięcej czasu chociaż czy aby na pewno bo w punkcje 7 mamy dwie zagnieżdżone pętle Byłoby to prawdą gdyby liczba iteracji pętli while z punktu 8 była co najwyżej logarytmicznie zależna od liczby punktów dla których znajdujemy otoczkę wypukłą

Mariusz: Jeżeli będziemy mieli funkcję porównującą punkty ze względu na obydwie współrzędne biegunowe (najpierw ze względu na kąt nachylenia do osi biegunowej a następnie względem odległości od bieguna) to z punktem 2 nie powinniśmy mieć problemu ? Gdybyśmy chcieli napisać jakąś ogólną funkcję sortującą to jako typ danych powinniśmy dać void * a dodatkowo funkcji w której następują porównania elementów należałoby przekazać wskaźnik do funkcji której chcemy użyć do porównywania jako parametr Trzynaście lat temu na algorytmach i strukturach danych wymagali algorytm Jarvisa i algorytm Grahama do wyznaczania otoczki wypukłej ale podobno są i inne np oparte na metodzie dziel i zwyciężaj Algorytm Jarvisa już znalazłem nawet z działającym kodem ale co z tymi innymi algorytmami

Pytający: Co do tego pierwszego pseudokodu (z CLRS...): to prawie to samo, co na ważniaku, a dokładnie to samo, o czym wcześniej Ci pisałem, czyli tu nie usuwamy punktów współliniowych, tylko sortujemy je w drugiej kolejności wg odległości od p₀ (punktu minimalnego). Pociąga to za sobą zmianę warunku przy zdejmowaniu ze stosu, o której też wcześniej pisałem (sprawdzamy, czy nie skręcamy w lewo zamiast sprawdzać, czy skręcamy w prawo). Co do funkcji z książki Sedgewicka: jesteś pewny, że wszystko dobrze przepisałeś? Masz z dodanym komentarzem, co sprawdzamy: int ccw(struct point p0, struct point p1, struct point p2) { int dx1,dx2,dy1,dy2; dx1 = p1.x – p0.x; dy1 = p1.y – p0.y; dx2 = p2.x – p0.x; dy1 = p2.y – p0.y; if (dx1*dy2 > dy1*dx2) return 1; // idąc p0−>p1−>p2 skręcamy w prawo if (dx1*dy2 < dy1*dx2) return −1; // idąc p0−>p1−>p2 skręcamy w lewo if ((dx1*dx2 < 0) | | (dy1*dy2)) return −1; // jeśli źle przepisałeś, to tę linijkę if ((dx1*dx1+dy1*dy1) < (dx2*dx2+dy2*dy2)) return 1; // tu z kolei porównujemy odległości (czy |p0p1|<|p0p2|) return 0; } Swoją drogą masz tu funkcję z Javy, tego samego autora (Sedgewick), tożsamą z napisaną przeze mnie uprzednio funkcją direction: /** * Returns true if a→b→c is a counterclockwise turn. * @param a first point * @param b second point * @param c third point * @return { −1, 0, +1 } if a→b→c is a { clockwise, collinear; counterclocwise } turn. */ public static int ccw(Point2D a, Point2D b, Point2D c) { double area2 = (b.x−a.x)*(c.y−a.y) − (b.y−a.y)*(c.x−a.x); if (area2 < 0) return −1; else if (area2 > 0) return +1; else return 0; } http://algs4.cs.princeton.edu/13stacks/Point2D.java.html Co do całego tego kopca i sortowania: przyczepiłbym się jedynie (mniejsza o nieintuicyjne nazwy zmiennych) do komentarza do SortowaniaStogowego, bo sortujemy tam tak naprawdę jedynie (n−1) elementów, nie n. Element A[0] jest przecież nieruszany, w kopcu indeksujemy od 1 dla łatwości obliczeń. Co do implementacji stosu: jeśli piszesz w C++, to do (de)alokacji używaj new/delete, nie malloc/free. Push() możesz krócej zapisać stack[++top]=p; "Co otrzymamy gdy w funkcji przesiewającącej operator porównania zastosowany do elementów tablicy zastąpimy twoją funkcją ?" Zależy, co sortujesz (usuwałeś punkty wspóliniowe czy nie) oraz którą funkcją. Ponownie odsyłam do: https://ideone.com/HENzFB (wciąż uważam, że działa ). Wiersze 29−32 to sortowanie, komparator napisałem tam jako lambdę, tak mi było wygodniej, acz równie dobrze mogłem napisać to jako funkcję i tu przekazać wskaźnik. W dokumentacji std::sort : http://en.cppreference.com/w/cpp/algorithm/sort można wyczytać, że comp ma zwracać true, jeśli a<b (tj. a ma być w posortowanym ciągu wcześniej niż b). Dlatego: w wierszu 30 obliczamy nasz skręt przy przejściu p0−>a−>b (lewo/prawo/prosto), a następnie w wierszu 31 jeśli d jest różne od zera (lewo/prawo) zwracamy informację, czy d>0 (czyli czy skręciliśmy w lewo, bo wtedy a<b w sensie kąta/polarności), a w przeciwnym przypadku (gdy d=0, tj. nie skręciliśmy) zwracamy informację, czy |p0a|<|p0b|, bo dla punktów współliniowych sortujemy wg odległości od p0. Co do wątpliwości odnośnie zagnieżdżonej pętli w algorytmie: przeczytaj jeszcze raz kilka ostatnich zdań z ważniaka, od "Przeanalizujmy teraz czas działania algorytmu". Co do ogólnej metody sortującej: w C++ masz coś takiego jak szablony, słowo kluczowe template. Patrz wyżej wrzucony link do dokumentacji std::sort, jest to "całkiem ogólna" funkcja. Quickhull: https://pl.wikipedia.org/wiki/Quickhull Tu masz metodę przyrostową, a na poprzednich stronach Graham/Jarvis, nie zaszkodzi przeczytać, jeśli wciąż czegoś nie rozumiesz: http://informatyka.wroc.pl/node/910?page=0,4

Mariusz: Gdy do porównywania użyłem zaproponowanych przez ciebie funkcji kod zatrzymuje się i jak dotąd nie wykryłem aby zwracał błędne wyniki Twoje wpisy w tym temacie były pomocne i nie wiem czy sam bym sobie poradził z tym drugim krokiem algorytmu Funkcja zaproponowana przez Sedgewicka jak zwykle działała błędnie Tutaj miałem problem z jednym krokiem algorytmu a właściwie z poprawnym porównywaniem punktów według współrzędnych biegunowych Napisałem w Pascalu i w Javie W Javie na Canvasie z MouseListenerem Próbowałem też przechwytywać wyjątek ale nie zawsze dawało to oczekiwany efekt w pewnych sytuacjach lepiej było zapobiec pojawieniu się błędu niż go później łapać wyjątkiem Zostaje jeszcze dopisać menu rozwijane z wyborem algorytmu (jak wcześniej napisałem algorytm Jarvisa już znalazłem) Jeśli chodzi o algorytm oparty o metodę dziel i zwyciężaj to tutaj przydałby się dokładniejszy opis i być może jakiś pseudokod zbliżony do tego co u Cormena i reszty dla algorytmu Grahama

Mariusz: Jeśli chodzi o algorytm sortowania przez scalanie to mamy void merge(int *A,int left,int mid,int right) { int leftSize,rightSize,i,j,k; int * B; //tę tablicę można przekazać jako parametr aby stale nie alokować i zwalniać pamięci leftSize=mid−left+1; rightSize=right−mid; B=(int *)malloc((leftSize+rightSize)*sizeof(int)); for(k=left;k<=right;k++) B[k−left]=A[k]; // Stosunkowo łatwo jest napisać wariant z połową tablicy pomocniczej i=0; j=n1; k=left; while((i<letfSize)&&(j<leftSize+rightSize)) { if(B[i]<=B[j]) { A[k]=B[i]; i++; } else { A[k]=B[j]; j++; } k++; } while(i<leftSize) { A[k]=B[i]; i++; k++; } /*Ta pętla dla tablic nie jest konieczna ale spróbujmy o niej zapomnieć podczas scalania pliku */ while(j<leftSlze+rightSize) { A[k]=B[j] j++; k++; } free(B); } void mergeSort(int *A,int left, int right) { int mid; if(left<right) { mid=left+(right−left)/2; mergeSort(A,left,mid); mergeSort(A,mid+1,right); merge(A,left,mid,right); } } Tylko jak zastosować ten kod do znajdowania otoczki ? Widziałem ten kod ale koleś jakoś niezbyt dokładnie opisał ten algorytm Nie widziałem też u niego pseudokodu funkcji scalającej dwie otoczki Wspomniał tylko o dwóch podejściach Bardziej skomplikowanym dzieleniu (z sortowaniem i poprowadzeniem prostej dzielącej zbiór punktów na mniej więcej równoliczne podzbiory) i mniej skomplikowanym scalaniu (wyznaczeniu czterech punktów na górze i na dole każdej z tych dwóch otoczek które należy połączyć a pozostałe punkty na tych dwóch otoczkach należy usunąć) Oraz z trywialnym dzieleniem i bardziej skomplikowanym scalaniem tutaj wspomniał że należy rozpatrzeć także przypadek gdy otoczki nie są rozłączne Co do tej funkcji Sedgewicka to w książce Algorithms in C , Dec 1990 p 350 wygląda ona tak int ccw(struct point p0,struct point p1,struct point p2) { int dx1,dx2,dy1,dy2; dx1=p1.x−p0.x; dy1=p1.y−p0.y; dx2=p2.x−p0.x; dy2=p2.y−p1.y; // Tutaj była literówka spowodowana metodą copy & paste if (dx1*dy2>dy1*dx2) return 1; if (dx1*dy2<dy1*dx2) return −1; if ((dx1*dx2<0) || (dy1*dy2 < 0)) return −1; // Tutaj wcześniej zapomniałem dać <0 if ((dx1*dx1+dy1*dy1) < (dx2*dx2+dy2*dy2) ) return 1; return 0; } Gdy uruchomiłem algorytm Grahama z funkcją znalezioną u Sedgewicka na testowej tablicy punktów to zostawiał mi jeden współliniowy punkt na otoczce który powinien usunąć

Mariusz: Funkcja Sedgewicka podsunęła mi pewien pomysł Jeżeli nie usuwamy punktów współliniowych w kroku 2 co dla tablic mogłoby zwiększyć złożoność to instrukcje iteracyjną for powinniśmy zmodyfikować tak aby zamknęła otoczkę sprawdzając wierzchołki cyklicznie przy czym zdejmowanie punktów powinniśmy zacząć już gdy będziemy mieli trzy punkty Warunek na instrukcję while powinniśmy zmodyfikować tak aby nie zdejmować ze stosu gdy na nim będzie mniej niż trzy elementy (gdy wchodzimy do pętli dwa elementy muszą być na stosie ponieważ funkcja sprawdzająca skręt pobiera z niego dwa elementy) Pomysł z zamykaniem otoczki pojawił się też w algorytmie Jarvisa który znalazłem w sieci wraz z kodem Jeśli chodzi o algorytm Jarvisa to na stronie gdzie go znalazłem zostawili komentarz do kodu niestety po rosyjsku a ja byłem zmuszany do angielskiego Co do innych algorytmów na ważniaku twierdzą że algorytm Grahama jest przykładem algorytmu przyrostowego Na ważniaku wspominają też o zamiataniu . Jak tego tutaj użyć ?

Mariusz: "Ach, i wcale nie musisz usuwać punktów współliniowych o mniejszej odległości od p0" Napisałem jak mi sugerowałeś ale zdaje się że pozostawienie tych punktów w kroku drugim algorytmu nie daje poprawnego wyniku dla tzw przypadków zdegenerowanych Zostawienie tych punktów spowoduje że pseudokod z CLRS trzeba będzie zmodyfikować bo np gdy wepchniemy na stos trzy elementy to już może okazać się że punkty są współliniowe Dobrze że podałeś te funkcje inaczej musiałbym użyć tej funkcji (ccw) Sedgewicka a po tym jak sprawdziłem że jego funkcja dla algorytmu Jarvisa (wrap) nie działa poprawnie miałem wątpliwości co do poprawności funkcji ccw Pisałeś aby użyć funkcji którą podałeś do sortowania a nie do porównywania, w przypadku tablicy do sortowania mamy kopiec Co do przypadków zdegenerowanych to w przypadku gdy użytkownik nie poda punktów program nie powinien nic wypisać w przypadku gdy użytkownik poda jeden punkt program powinien go wypisać w przypadku gdy użytkownik poda punkty które są współliniowe program powinien wypisać punkty będące końcami najkrótszego odcinka zawierającego podane punkty

Pytający: Co do Quickhulla: przecież w podanym linku masz pseudokod, z czym masz problem? Jakich struktur danych użyć? Punkty proponuję przechowywać na liście, wtedy masz łatwość "sklejania" wyników wywołań rekurencyjnych. Co do MergeSorta: co trzeba zmienić? 1. Chcesz sortować punkty, nie inty, więc musiałbyś zmienic typ danych w tablicy. 2. Punkty inaczej porównujesz, więc musiałbyś odpowiednio zmodyfikować wszystkie porównania elementów. Zdaje się, że porównania występują jedynie w linijce: if(B[i]<=B[j]) 3. Przed sortowaniem oczywiście znajdujesz punkt minimalny, wrzucasz go na pierwsze miejsce w tablicy, więc sortowanie wywołujesz: mergeSort(jakasTablica, 1, n−1), gdzie n to rozmiar tejże tablicy. Co do scalania dwóhc otoczek: nie bardzo rozumiem, o czym mówisz. Po co chcesz scalać otoczki? O jakim algorytmie mowa? Jeśli odnosisz się do MergeSorta, tam sortujemy (i scalamy w trakcie) zbiory punktów, niekoniecznie będące otoczkami. Co do funkcji: int ccw(struct point p0,struct point p1,struct point p2) { int dx1,dx2,dy1,dy2; dx1=p1.x−p0.x; dy1=p1.y−p0.y; dx2=p2.x−p0.x; dy2=p2.y−p1.y; if (dx1*dy2>dy1*dx2) return 1; if (dx1*dy2<dy1*dx2) return −1; if ((dx1*dx2<0) || (dy1*dy2 < 0)) return −1; if ((dx1*dx1+dy1*dy1) < (dx2*dx2+dy2*dy2) ) return 1; return 0; } Liczy ona: if (dx1*dy2>dy1*dx2) return 1; // idąc p0−>p1−>p2 skręcamy w lewo (counterclockwise) if (dx1*dy2<dy1*dx2) return −1; // idąc p0−>p1−>p2 skręcamy w prawo (clockwise) // jeśli żaden z powyższych ifów nie jest spełniony, mamy 3 punkty współliniowe i: if ((dx1*dx2<0) || (dy1*dy2 < 0)) return −1; // jeśli p0 jest pomiędzy p1 i p2, tj. idąc p0−>p1−>p2 w punkcie p1 zawracamy, a punkt p2 jest po przeciwnej stronie p0; w algorytmie Grahama taka sytuacja nigdy nie wystąpi, bo jako p0 zawsze mamy w porównaniu punkt minimalny, więc nawet gdy mamy punkty współliniowe p1 i p2 będą "po tej samej stronie", dlatego w mojej metodzie od razu sprawdzałem odległość if ((dx1*dx1+dy1*dy1) < (dx2*dx2+dy2*dy2) ) return 1; // jeśli |p0p1|<|p0p2| Zatem jak dla mnie brakuje jeszcze sprawdzenia przypadku, gdy |p0p1|>|p0p2|, wtedy należałoby zwrócić −1. I dopiero w przeciwnym przypadku (do wszystkich poprzednich) return 0;, czyli gdy p1==p2. Acz oczywiście niekoniecznie musi tego brakować − zależy, do czego ta funkcja była użyta... Co do zamiatania: nie wiem, czy jakiś algorytm dokładny z tego korzysta. Na pewno jest aproksymacyjny: http://geomalgorithms.com/a11-_hull-2.html Co do przypadków "zdegenerowanych": faktycznie, algorytm może się wykrzaczyć bez wyrzucania punktów współliniowych, ale jedynie w przypadku, gdy po posortowaniu pierwsze co najmniej 4 punkty (włącznie z punktem minimalnym) są współliniowe. Wtedy: najpierw wrzucimy do otoczki pierwsze 3 punkty (współliniowe), w efekcie kolejno zdejmiemy ze stosu (otoczki) punkty trzeci i drugi, bo nie będziemy mieli skrętu w lewo (gdyż punkt czwarty jest współliniowy z poprzednimi), co doprowadzi do pozostawienia na stosie jedynie punktu minimalnego, co nie powinno mieć oczywiście miejsca. Można by tego uniknąć gwarantując, że pierwsze trzy punkty faktycznie nie są współlinowe. Dodatkowo, jeśli punkt minimalny jest współliniowy z 2 ostatnimi z otoczki wynikowej, pewnie chciałbyś usunąć ostatni punkt, czego tu nie robimy w takiej sytuacji. Najprosćiej chyba byłoby jednak pousuwać te współliniowe punkty przy sortowaniu. A jeśli masz mniej niż 3 punkty, to Grahama w ogóle nie wywołujesz, obsłuż to oddzielnie.

Mariusz: Pisałem o pomysłach na scalanie przedstawionych na tej stronie http://informatyka.wroc.pl/node/910?page=0,4 Jeśli chcielibyśmy usuwać punkty współliniowe to chyba najlepiej byłoby posortować punkty względem kąta przeciwnie do ruchu wskazówek zegara a względem odległości od bieguna malejąco Widziałem taki algorytm i dla posortowanego ciągu (zarówno tablicy jak i listy) będzie działał w czasie O(n) czyli nie zwolni algorytmu zbytnio Algorytm wymaga porównywania wystarczy tylko sprawdzanie czy równe czy różne i nie wiem czy twoja funkcja wystarczy i jak jej użyć

Mariusz: https://ideone.com/vvBi4A Jeśli chodzi o algorytm Grahama to oto co udało się napisać z wykorzystaniem pseudokodu CLRS Introduction to Algorithms 3rd edition , funkcji które zaproponowałeś i funkcji usuwającej powtórzenia znalezionej w sieci Ścieżki do plików można by podać jako argumenty funkcji main Nie pomyślałem o tym zanim wrzuciłem kod Co do funkcji usuwającej powtórzenia to lepiej byłoby gdyby ta funkcja je przesuwała na koniec tablicy zamiast nadpisywać na wypadek gdybyśmy tę otoczkę chcieli narysować Moje pomysły na poprawienie tej funkcji zwiększają złożoność kodu czasową bądź pamięciową i ciekawy jestem jak ją poprawić aby miała złożoność T(n)=O(n) , M(n)=O(1) Znasz rosyjski ? Na rosyjskiej stronie znalazłem kod algorytmu Jarvisa Nie testowałem go we wszystkich możliwych przypadkach ale wygląda na to że działa poprawinie Do kodu dołączony był komentarz w języku rosyjskim

Adamm: podaj tą rosyjską stronę

Pytający: Cóż, pierwsza myśl: punkty współliniowe moglibyśmy usuwać już w trakcie sortowania, w końcu tam już je porównujemy. Część z nich moglibyśmy już wyeliminować podczas przywracania własności kopca od dołu, tj. jeśli przy naprawianiu po drodze napotkamy punkty współliniowe z p0, ten bliższy p0 można by wyrzucić (zamienić miejscem z ostatnim elementem kopca, zmniejszyć o 1 rozmiar kopca i naprawiać dalej w ten sposób). W ten sposób przed właściwym sortowaniem możliwe, że trochę byśmy uszczuplili zbiór punktów, jednak mogłyby wciąż zostać jakieś punkty współliniowe z p0. Resztę można by usunąć już sortując, tj. zdejmując kolejne korzenie kopca (dla punktów współliniowych najpierw zdejmiemy ten najbardziej odległy). Wtedy przy zdejmowaniu sprawdzamy współliniowość punktów p0, właśnie zdjętego korzenia kopca oraz poprzedniego zdjętego korzenia, który nie był współliniowy. Jeśli mamy punkty współliniowe, właśnie zdjęty korzeń kopca wyrzucamy, w przeciwnym razie dodajemy do posortowanego ciągu punktów. Jednak jest problem − raczej nie zrobisz tego jednocześnie: bez nadpisywania, bez zwiększenie złożoności czasowej i "w miejscu" (O(1) pamięciowo). Przynajmniej osobiście nie dostrzegam takiego rozwiązania. Zatem ja bym to zrobił używając dodatkowego stosu (O(n) pamięciowo), pseudokod: A − nasza tablica posortowanych punktów, gdzie A[0] to min, a zakres [1..n−1] jest posortowany względem A[0] biegunowo rosnąco przeciwnie do ruchu wskazówek zegara i rosnąco względem odległości S=new Stos<int>; // stos indeksów S.push(n−1); for(int i=n−2;i>0;−−i) { if(direction(A[0],A[i],A[S.top()])!=0) S.push(i); } S.push(0); W ten sposób uzyskamy stos z indeksami elementów posortowanych, bez indeksów zbędnych punktów współliniowych. Wtedy podczas tworzenia otoczki należałoby korzystać z tego stosu (najpierw upewnić się, że są tam przynajmniej 3 punkty) do pobierania kolejnych indeksów, pseudokod: hull.add(A[S.pop()]); // pierwsze 3 punkty otoczki hull.add(A[S.pop()]); hull.add(A[S.pop()]); while(!S.isEmpty()) { // bez punktów współliniowych wystarczy sprawdzać "direction(...)<0" while(direction(hull[last−1],hull[last],A[S.top()])<0) hull.removeLast(); hull.add(A[S.pop()]); }

Mariusz: Tak sobie pomyślałem że pomysł z dodatkową pamięcią jest akceptowalny w tym przypadku bo i tak korzystamy z dodatkowej tablicy przeznaczonej na stos i można by właśnie tę pamięć wykorzystać do zapamiętywania nadpisanych elementów Pomysł polegał na tym aby nadpisywane elementy zapamiętać w tablicy przeznaczonej na stos i po zakończeniu pętli która usuwała powtórzenia dopisać zapamiętane elementy na końcu tablicy Dla mnie wygodniej chyba będzie gdy punkty będą posortowane biegunowo względem kąta przeciwnie do ruchu wskazówek zegara a względem odległości malejąco bo zostawiamy wtedy pierwsze wystąpienie elementu Twój pomysł z usuwaniem w trakcie sortowania nie będzie działał ? Na pierwszy rzut oka wyglądał ciekawie Najlepiej abyśmy po usuwaniu dostali tablice podzieloną na dwie podtablice gdzie podtablica 1..m−1 nie zawiera powtórzeń natomiast podtablica m..size−1 zawiera tylko powtórzenia Sedgewick proponuje trzymać punkty należące do otoczki w tej samej tablicy co wszystkie punkty i zwracać indeks pierwszego punktu nie należącego do otoczki wtedy podprogram usuwający punkty współliniowe musiałby mieć T(n)=O(n) M(n)=O(1) aby nie skomplikować kodu Co do algorytmu Jarvisa to znalazłem go wraz z kodem na stronie Вера Господарец Уроки программирования на языке Паскаль Построение выпуклой оболочки Komentarz do kodu jest po rosyjsku Translatory kiepsko tłumaczą a mamuśka skoro nie chciała uczyć to tym bardziej nie przetłumaczy

Adamm: Вера Господарец to jest jakieś imię Уроки программирования на языке Паскаль uroki programowania w języku paskal Построение выпуклой оболочки Построение nie wiem co to znaczy, ale dalej jest o wypukłej otoczce

Adamm: Построение выпуклой оболочки znaczy "budowanie wypukłej otoczki" czy coś takiego

Adamm: pomyłka Уроки − lekcje ogólnie to rosyjskiego nie znam, ale znam cyrylicę "domyśliłem się" co większość znaczy, i taki tego efekt

Mariusz: Gdybyś wpisał ten tekst napisany cyrylicą do przeglądarki to wyskoczyłaby ci ta lekcja ale skoro nie uczyłeś się rosyjskiego to będziesz miał problem z przetłumaczeniem ale mimo to dzięki za chęci Jak chcesz sprawdzić ile zrozumiesz bez znajomości rosyjskiego to zajrzyj na stronę do której odnośnik wkleiłem poniżej http://gospodaretsva.com/urok-35-postroenie-vypukloj-obolochki.html

Adamm: Урок из серии “Геометрические алгоритмы” lekcje z serii "geometryczne algorytmy" Вычисление выпуклой оболочки важно не только само по себе, но и как промежуточный этап для многих задач вычислительной геометрии. wyznaczenie obłoczki wypukłej ważne jest nie tyle samo dla siebie, ale jako przejściowy etap dla zadań geometrii komputerowej Например, задача о наиболее удаленных точках. na początek, zadanie o najbardziej oddalonych punktach Дано множество из N точек. dany jest zbiór punktów − N Нужно выбрать пару максимально удаленных друг от друга точек. należy wybrać pary maksymalnie oddalonych punktów конечного числа точек N называется наименьший, выпуклый многоугольник, содержащий все точки из N (некоторые из точек могут быть внутри многоугольника, некоторые на его сторонах, а некоторые будут его вершинами). końcową liczbę punktów N nazywamy najmniejszym, wypukłym wielokątem, zawierającym wszystkie punkty ze zbioru N (niektóre z punktów mogą być wewnątrz wielokąta, niektóre na jego bokach, a niektóre na jego wierzchołkach) Наглядно это можно представить себе так: в точках N вбиваются гвозди, на которые натянута резинка, охватывающая их все – эта резинка и будет выпуклой оболочкой множества гвоздей. można to sobie wyobrazić tak: w N punktach wbijamy gwoździe, na których rozciągamy gumę, obejmując je wszystkie − ta gumka będzie wypukłą obłoczką zbioru gwoździ Задача. На плоскости задано множество S точек. Найти вершины выпуклой оболочки этого множества. zadanie. na płaszczyźnie mamy zbiór punktów − S. znaleźć wierzchołki wypukłej obłoczki tego zbioru Будем перечислять вершины в порядке обхода против часовой стрелки. Для эффективного решения этой задачи существует несколько различных алгоритмов. Приведем наиболее простую реализацию одного из них – алгоритма Джарвиса. Этот алгоритм иногда называют «заворачиванием подарка». będziemy wymieniać boki w kolejności przeciwko wskazówkom zegara. dla efektywnego "ruszenia" tego zadania potrzebnych jest kilka różnych algorytmów. jedna z najbardziej prostych realizacji tego planu − algorytm Jarvisa czasami nazywa się ten algorytm "zawiązywaniem prezentu" (?) Перечисление точек искомой границы выпуклого многоугольника начнем с правой нижней P₁, которая заведомо принадлежит границе выпуклой оболочки. poszukiwanie punktów pożądanych granic wypukłego wielokąta zaczynamy z prawego dolnego punktu P₁, który oczywiście należy do brzegu wypukłej obłoczki. Обозначим ее координаты (x₁; y₁) oznaczmy jego współrzędne (x₁; y₁) Следующей при указанном порядке обхода будет точка P₂(x₂; y₂) następnie według określonej kolejności będzie punkt P₂(x₂; y₂) Она, очевидно, обладает тем свойством, что все остальные точки лежат слева от вектора P₁P₂ on, oczywiście, ma własność, że wszystkie inne punkty leżą na lewo od wektora P₁P₂ т.е. ориентированный угол между векторами P₁P₂ и P₁M неотрицателен для любой другой точки М нашего множества. to znaczy, zorientowany kąt między wektorami P₁P₂ i P₁M jest nieujemny dla każdego innego punktu M naszego zbioru Для кандидата на роль точки P₂ проверяем выполнение условия [P₁P₂; P₁M]≥0 со всеми точками М. dla kandydata na rolę punktu P₂ sprawdzić warunek [P₁P₂; P₁M]≥0 ze wszystkimi punktami M Если точек, удовлетворяющих этому условию несколько, то вершиной искомого многоугольника станет та из них, для которой длина вектора P₁P₂=(x₂−x₁;y₂−y₁) максимальна. jeśli punktów, spełniających ten warunek jest kilka, to na górze tego wielokąta stanie ten z nich, dla którego długość wektora P₁P₂ jest maksymalna Будем поступать так и далее. będziemy postępować tak dalej Допустим, уже найдена i−я вершина P_i выпуклой оболочки. Для следующей точки P_i+1 косые произведения [P_iP_i+1; P_iM] не отрицательны для всех точек М. załóżmy, że znaleźliśmy i−ty wierzchołek P_i wypukłej obłoczki. dla następnych punktów P_i+1 (długość iloczynu wektorowego) [P_iP_i+1; P_iM] są ujemne dla wszystkich punktów M. Если таких точек несколько, то выбираем ту, для которой вектор P_iP_i+1 имеет наибольшую длину. jeśli takich punktów jest kilka, to wybieramy te, dla których wektor P_iP_i+1 jest najdłuższy Непосредственно поиск такой точки можно осуществить так. Сначала мы можем считать следующей (i+1)−й, любую точку. bezpośrednio można takich punktów szukać tak najpierw możemy odczytać następny (i+1)−szy, dowolny punkt Затем вычисляем значение [P_iP_i+1; P_iM] , рассматривая в качестве М все остальные точки. Если для одной из них указанное выражение меньше нуля, то считаем следующей ее и продолжаем проверку остальных точек (аналогично алгоритму поиска минимального элемента в массиве). następnie obliczyć wartość [P_iP_i+1; P_iM], rozważając wszystkie M innych punktów. jeśli dla jednej z nich wyrażenie będzie mniejsze od zera, to rozważamy to, i kontynuujemy sprawdzanie kolejnych punktów (analogicznie do algorytmu szukania minimalnego elementu w tablicy) Если же значение выражения равно нулю, то сравниваем квадраты длин векторов. Продолжая эту процедуру, мы рано или поздно вернемся к точке P₁. jeśli wyrażenie jest zerem, to porównaj kwadraty długości wektorów. podążając tą procedurą, my prędzej czy później wrócimy do punktu P₁. Это будет означать, что выпуклая оболочка построена. to będzie oznaczać, że zbudowaliśmy wypukłą obłoczkę Приведем программу решения данной задачи для целочисленных координат. podajemy program rozwiązujący ten problem dla liczb całkowitych Множество исходных точек находится в массиве a, а все точки, принадлежащие выпуклой оболочке, будем записывать в массив b. zbiór początkowych punktów znajduje się w tablicy a, a wszystkie punkty, należące do wypukłej obłoczki, będą zapisane w tablicy b tyle mi się udało przetłumaczyć, mam nadzieję że jest to przynajmniej choć trochę zrozumiałe

Adamm: i to co było w kodzie Квадрат длины вектора − kwadrat długości wektora Построение выпуклой оболочки − zbudowanie wypukłej obłoczki ищем правую нижнюю точку − szukam prawego niższego punktu запишем ее в массив b и переставим на первое место в массиве a − zapisuję je w tablicy b i przestawiam na pierwsze miejsce w tablicy a ищем очередную вершину оболочки − szukam następnego wierzchołka obłoczki записана очередная вершина − zapisany następny wierzchołek пока ломаная не замкнется − aż łamana nie zostanie zamknięta количество точек − liczba punktów Входные данные − wejście Выходные данные − wyjście

Mariusz: Adam nieźle się spisałeś ciekawy byłem tego komentarza do kodu (nie tylko w samym kodzie ale i tej lekcji) Adam gdybyś miał sam napisać kod algorytmu Jarvisa to wystarczyłoby tobie to co po rosyjsku było napisane ? Co do usuwania powtórzeń w posortowanej tablicy to widziałem u pewnego kolesia pewien kod int RemoveDuplicates(int a[],int size) { int prev=0; for(int i = 0;i<size; ++i) { if(a[i]!=a[prev]) a[++prev] = a[i]; } int count = prev + 1; return count; } W instrukcji warunkowej if występuje nadpisywanie elementów przez co możemy zgubić elementy które później mogłyby być przydatne przy rysowaniu otoczki Czy gdybyśmy nadpisywanie elementu o indeksie prev+1 elementem o indeksie i zastąpili zamianą elementu prev+1 z elementem i to nie popsulibyśmy sobie algorytmu Zamieniając elementy nie tracimy powtórzenia , zamiana jest wykonywana w czasie stałym oraz wymaga stałej ilości pamięci więc nie zwiększymy sobie złożoności tylko czy aby na pewno algorytm będzie nadal poprawny

Pytający: Nie możesz zamieniać elementów zamiast nadpisywania, bo wtedy nie masz już gwarancji, że punkty w pozostałej części tablicy (kopca) wciąż są odpowiednio posortowane, co psuje algorytm. Właśnie dlatego wyżej pisałem, że: "raczej nie zrobisz tego jednocześnie: bez nadpisywania, bez zwiększenia złożoności czasowej i "w miejscu" (O(1) pamięciowo)". Z czegoś trzeba zrezygnować. Jeśli nie potrzebujesz pamiętać punktów nienależących do otoczki − śmiało możesz nadpisywać usuwając punkty współliniowe, a jeśli jednak chcesz wciąż mieć wszystkie punkty, lepiej skorzystać z dodatkowej pamięci (stos/lista/dodatkowa tablica − jak Ci wygodnie, nie powinno być więcej jak O(n)), niż zwiększyć złożoność czasową.

Mariusz: Jeżeli chodzi o podejście listowe to mam na razie takie funkcje struct Node { int x,y; struct Node *next; }; //funkcje do obsługi stosu void createList(struct Node **head) { (*head)=NULL; } int isEmpty(struct Node *head) { return (head==NULL); } void push(struct Node **head,int xcoord,int ycoord) { struct Node *p; p=(struct Node *)malloc(sizeof(struct Node )); p−>x=xcoord; p−>y=ycoord; p−>next=(*head); (*head)=p; } void pop(struct Node **head) { struct Node *p; if((*head)!=NULL) { p=(*head); (*head)=(*head)−>next; free(p); } } /*Funkcja wstawiająca węzeł w sposób uporządkowany jednak zbyt wolna jak dla potrzeb tego algorytmu */ void ListInsert(struct Node **head,int xcoord,ycoord) { struct Node *px; struct Node *py; struct Node *pz; px=(struct Node *)malloc(sizeof(struct Node)); px−>x=xcoord; px−>y=ycoord; if((*head)==NULL) { (*head)=px; px−>next=NULL; } else { py=(*head); pz=NULL; while(py!=NULL && px−>y>py−>y) { pz=py; py=py−>next; } if(pz==NULL) { px−>next=(*head); (*head)=px; } else { px−>next=py; pz−>next=px; } } } /* Wyszukiwanie elementu na liście o zadanym kluczu */ struct Node * searchNode(struct Node *head, int key) { struct Node *p=head; while(p!=NULL && p−>y!=key) p=p−>next; return p; } /* Sortowanie listy przez scalanie Dla listy dwukierunkowej trzeba jeszcze odpowiednio poustawiać wskaźniki prev W przypadku listy dwukierunkowej można też nieco przyśpieszyć funkcję rozdzielającą Gdybyśmy chcieli usunąć rekurencję to trzeba by było skorzystać z pomysłów znanych z sortowania plików tj sortowania przez łączenie proste bądź sortowania przez łączenie naturalne */ void split(struct Node *head,struct Node **front,struct Node **back) { struct Node *slow; struct Node *fast; if(head==NULL || head−>next==NULL) { (*front)=head; (*back)=NULL; } else { slow=head; fast=head−>next; while(fast!=NULL) { fast=fast−>next; if(fast!=NULL) { slow=slow−>next; fast=fast−>next; } } (*front)=head; (*back)=slow−>next; slow−>next=NULL; } } struct Node * sortedMerge(struct Mode *p,struct Node *q) { struct Node *newHead=NULL; struct Node *sorting; if(p==NULL) return q; if(q==NULL) return p; if(p−>y<=q−>y) { sorting=p; p=sorting−>next; } else { sorting=q; q=sorting−>next; } newHead=sorting; while(p!=NULL && q!=NULL) { if(p−>y<=q−>y) { sorting−>next=p; sorting=p; p=sorting−>next; } else { sorting−>next=q; sorting=q; q=sorting−>next; } } if(p==NULL) sorting−>next=q; else sorting−>next=p; return newHead; } void mergeSort(struct Node **head) { struct Node *h1=NULL; struct Node *h2=NULL; if((*head)!=NULL && (*head)−>next!=NULL) { split((*head),&h1,&h2); mergeSort(&h1); mergeSort(&h2); (*head)=sortedMerge(h1,h2); } } void reverse(struct Node **head) { struct Node *p=NULL; struct Node *q=(*head); struct Node *r=NULL; if(q!=NULL) r=q−>next; while(q!=NULL) { q−>next=p; p=q; q=r; if(r!=NULL) r=r−>next; } (*head)=p; } /* Znalazłem jeszcze funkcję do usuwania powtórzeń ale mam wątpliwości co do jej poprawności zwłaszcza co do obsłużenia przypadków brzegowych i możliwych błędów */ /* Co do sortowania to chyba wygodniejsza będzie wersja iteracyjna algorytmu Aby ten algorytm przepisać w postaci iteracyjnej trzeba by chyba skorzystać z pomysłów na sortowanie plików tj sortowanie przez łączenie proste albo sortowanie przez łączenie naturalne Warunkem końca byłoby to czy po rozdzieleniu serii dostajemy pustą listę */

Ambitny: Ciekawa jest ta cała dyskusja. Obecnie jestem na etapie przerabiana Cormena, widzę że sporo osób tutaj zna się na algorytmach

Mariusz: Ambitny pseudokod algorytmu Grahama można znaleźć u Cormena pod warunkiem że korzystasz z nowszego wydania bo te co krąży po sieci jest trochę za stare chyba że czytasz Cormena po angielsku wtedy w trzecim wydaniu które jest dostępne w sieci są elementy geometrii obliczeniowej

Ambitny: Tak, korzystam z angielskiej wersji, tam to powinno być. Dopiero zacząłem, tak jak pisałem wyżej. Mariusz, a co myślisz o książce Algorytmy − Sanjoy Gupta?

Mariusz: Ja tylko przeglądałem CLRS Introduction to Algorithms Wirth Algorithms+Data structures=Programs Banachowski Diks Rytter Algorytmy i struktury danych Sedgewick Algorithms in C Ja tak właściwie algorytmy miałem ok 13 lat temu i chciałem sobie trochę przypomnieć Moje notatki były spisane w kiepskiej jakości zeszycie Ambitny w jakim momencie jesteś ? Sortowanie i wyszukiwanie ? Algorytmy z powrotami ? Struktury danych takie jak stos, kolejka, czy lista ?

Mariusz: W podejściu listowym punkt 1 można by zrealizować tak że usuwamy dowiązania punktu o najmniejszej współrzędnej rzędnej i odciętej jeśli jest więcej niż jeden punkt o tej samej rzędnej i wstawiamy go na początek listy Sortujemy punkty biegunowo przez scalanie (tutaj wygodniejsza w użyciu byłaby chyba wersja iteracyjna) Usuwamy dowiązania powtórzeń i zapamiętujemy wskaźnik na ogon , węzły których dowiązania usunęliśmy łączymy ze sobą i dołączamy na koniec listy Jeżeli piszemy funkcję do usuwania powtórzeń to zwraca ona ten zapamiętany ogon Dalej to zabawa ze stosem

Ambitny: Mariusz, przedmiot dopiero mi się rozpoczął na studiach. Jestem po notacji O dopiero. Teraz zaczynamy drugi dział. Jeszcze nie wiem jaką ma zawartość, więc się nie wypowiem. My mamy książke raczej taką dla matematyków. Coś obliczyć, udowodnić, rzadziej takie rzeczy typu stos czy kolejki. Przynajmniej na razie nic nie było o tym mówione.

Ambitny: Przedmiot to al. i struktury danych, to się akurat zgadza, jeśli chodzi o nazwe.

Mariusz: Jarvis − na podstawie tego kodu na stronie którą Adam tłumaczył https://ideone.com/aVir3z Quick Hull − na podstawie algorytmu przedstawionego gdzieś w sieci https://ideone.com/qDhW0w Co do Grahama to na tej liście brakuje funkcji realizujących punkt 2 algorytmu przedstawionego w CLRS Introduction to Algorithms a przetłumaczonego mniej lub bardziej dokładnie na ważniaku Co do sortowania to myślałem nad łączeniem naturalnym Przydałaby się też funkcja usuwająca powtórzenia (tutaj wystarczyłoby powtórzenia wstawiać na koniec listy a zwrócić wskaźnik na ogon podlisty bez powtórzeń) Myślałem aby funkcję porównującą przekazać jako argument funkcji sortującej i usuwającej powtórzenia

Mariusz: Punkty przechowywać na liście czy w tablicy ? Banachowski, Diks , Rytter w swojej książce o algorytmach i strukturach danych zaproponowali cykliczną listę dwukierunkową jako strukturę danych jednak nie wiem jak mogłaby taka lista wyglądać Skoro wybraliśmy tablicę to moglibyśmy ją posortować gotowcem z stdlib tylko jak wyglądałyby parametry wywołania ponieważ pierwszego elementu (tego o indeksie zero) nie sortujemy a i twoja funkcja porównująca nie pasuje do tego gotowca z stdlib

Pytający: "a i twoja funkcja porównująca nie pasuje do tego gotowca z stdlib" Czyli chyba do mnie to kierujesz... jak już mówiłem, zakończyłem z Tobą wszelakie dyskusje.