Wykladnicza i logarytmiczne 5-latek: Jednokladnosc o srodku O i stosunku k to przeksztalcenie plaszczyzny w ktorym obrazem punktu P jest taki punkt P ' ze OP'= k*OP Powinowactwo prostokatne o osi s i stosunku k to takie przeksztalcenie plaszczyzny gdzie obrazem punktu P jest punkt P' ze MP' = k*MP gdzie M jest rzutem prostokatnym punktu P na prosta s zawana osia powinowactwa Teraz jesli osia powinowactwa jest os OX i punkt P ma wspolrzedne (x,y) to P' ma wspolrzedne x'= x i y'= k*y Punkt M= (x,0) Teraz jesli osia powinowactwa jest os OY to i p=(x,y) to punkt P' ma wspolrzedne x'= k*x i y'=y Jest mi to potrzebne do zadania Sporzadz wykres funkcji y=2^x (to zrobie Podaj wzor funkcji ktorej wykres otrzymasz z wykresu y=2^x przez przeksztalcenie a) symetria wzgledem osi Ox ( tutaj bedzie y=−2x

	1		1
b) symetria wzgledem osi OY (tutaj bede mial y= 2−x=		= (		)x
	2x		2

c) symetria wzledem punktu 0 ( y=−0,5^x Translacje to wiem Teraz wlasnie jednokladnosc d) jednokladnosc o stosunku s e) jednokladnosc o stosunku s i srodku 0 f) powinowactow o stosunku s wzgledem OX i g) powinowactwo o stosunku s wzgledem OY Tutaj prosilbym o wytlumaczenie

5-latek: Potrzebne potem do nastepnego zadania Wyznaczyc funkcje odwrotna do y=2^x i te same przeksztalcenia Symetrie i translaceje to wiem funkcja odwrotna bedzie tutaj y=log₂x

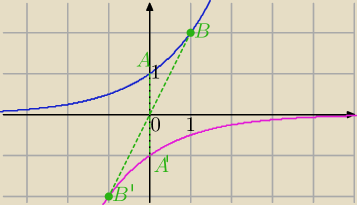
Mila: a) y=−2^x c) symetria względem punktu (0,0) to obrót o 180 ^o. ( są wzory na obrót) y=2^x x'=−x⇔x=−x' y'=−y⇔y=−y' −y'=2^−x'

	1
y=−(		)x
	2

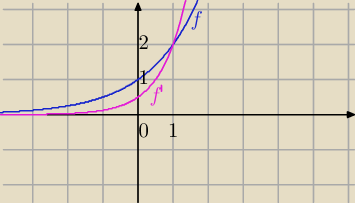
Mila: e) jednokładność o stosunku s i środku S(0 ,0)

	1
Weźmy s=
	2

P(x,y) − dany punkt wykresu y=2^x

	1
x'=		x ⇔x=2x'
	2

	1
y'=		y⇔y=2y'
	2

Podstawiamy do wzoru funkcji 2y'=2^2x'

	1
y'=		*4x'
	2

	1
y=		*4x
	2

=========

5-latek: dzien dobry Milu Trawie to na razie .

Mila:

	1
e) s=−
	2

	1
x'=−		x⇔x=−2x'
	2

	1
y'=−		y⇔y=−2y'
	2

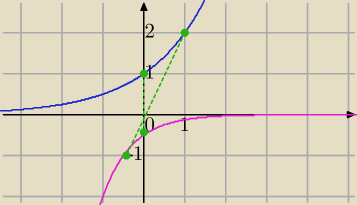
f(x)=y=2^x −2y'=2^−2x'

	1		1
y'=−		*(		)x
	2		4

P(1,2)

	1		1		1
P'=(−		,−		*2)=(−		,−1)
	2		2		2

Mila: Reszta po kolacji.

5-latek: Dobrze .

5-latek: Zastanawiam sie dlaczego wstawilem sama jednolkladnosc skoro w jednokladnosci musi byc srodek W obrocie jest tak x'= xcosφ−ysinφ y'= xsinφ+y cosφ Dla kąta 180^o sinφ=0 cosφ=−1 Z tego mam x'=−x y'=−y

Milo: Mogę też spróbować? f) Jeśli zrzutujemy punkt P(x,y) na oś OX, dostaniemy punkt M (x,0) MP = [0,y] MP' = [0, sy] Czyli jak napisałeś, x'=x oraz y'=sy

	y'
Stąd y=
	s

y=2^x

	y'
Podstawiajac		= 2x'
	s

y' = s*2^x' y = s*2^x

5-latek: Wzorujac sie na Twoich obliczeniach f) x'=x to to x=x'

	y'
y'= s*y to y=
	s

y'
	= 2x'
s

	2x'
y'=
	s

	2x
y=
	s

	x'
g) x'= s*x ⇒x=
	s

y'=y to y=y' Postawiam do wzoru y'= 2^x'/s y= 2^x/s Powinno byc ok . (prosze sprawdz po kolacji

5-latek: No jasne ze w f) y=s*2^x Jak ja to liczylem

5-latek: Oczywiscie ze mozesz sprobowac .

Milo: g) mi wyszło tak samo ^^

5-latek: Wiec tutaj po prostu trzeba znac definicje i wzory .

Milo: y=log₂x e) skala s, środek S(0,0) niech P=(x,y) SP=[x,y] SP'=s[x,y] = [sx,sy] P' = (sx, sy) x'=sx oraz y'=sy

	x'		y'
x=		oraz y=
	s		s

y'		x'
	= log2		= log2x' − log2s
s		s

y' = s*log₂x' − s*log₂s Z tego co porysowałem w Geogebrze nawet się zgadza

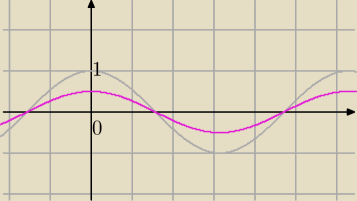
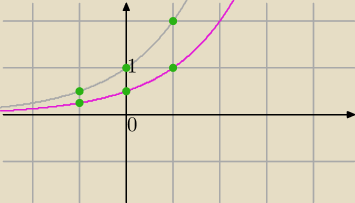
Mila: f) powinowactwo o stosunku s względem OX

	1
s=
	2

x'=x

	1
y'=		y
	2

Często wykorzystywane przy Przykłady:

	1
1) y=		cos(x) ( "skrócenie" wykresu)
	2

5-latek: Dziekuje CI bardzo Milu

Mila:

	1
2) y=		*2x
	2

5-latek: Milu Jesli mozesz to proszse abys napisala jak narysowac tutaj np wykres funkcji y=log₂x ?

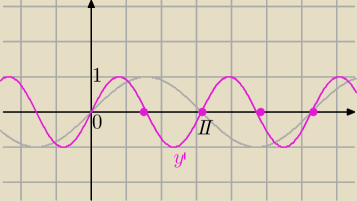
Mila: g)Powinowactwo o stosunku s względem OY

	1
s=
	2

	1
x'=		x⇔x=2x'
	2

y'=y Tu będzie zagęszczenie wykresu ( szybko zbliżamy się do osi OY) y=sinx y'=sin(2x')

5-latek: Za wszystkie cenne uwagi jeszcze raz dziekuje

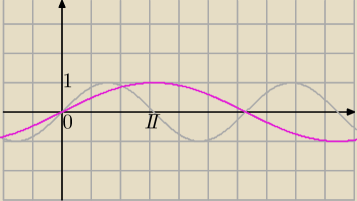
Mila: Do wpisu 20:18 y=sin(2x)

	2π
T=		=π
	2

g) s=2

	1
x'=2x⇔x=		x'
	2

y'=y y=sinx

	1
y'=sin(		x') (rozszerzenie wykresu w poziomie)
	2

	2π
T=		=4π
	1   2

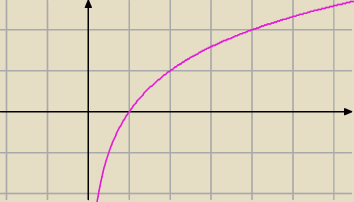
Mila: wpisujesz: (ln(x))/(ln(2))