Iloczyn skalarny na podstawie długości wektorów Alglin: Mamy podane długości wektorów: |U| = 2 |V| = 3 |U+V|= 4 Mam obliczyć iloczyn skalarny U i V I kurde próbowałem dostatecznie długo, żeby zrozumieć że jednak nie mam pojęcia jak to zrobić :S

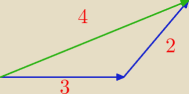
Adamm: U•V=|U||V|*cosα twierdzenie Cosinusów

Alglin: ej proste, nie znałem tego dzięki. skalarny wyszedł mi ⁻²₃, o to chodziło?

Adamm: −3/2

Alglin: yy tak, bląd przy wpisywaniu, −3/2 zgadza się, a co jest kiedy mamy podany |U−V|? Wtedy kolejność boków się zmienia, więc liczymy cosinus kąta, który nie jest nam potrzebny. Np |U|=4 |V|=5 i |U−V|=1. Co wtedy?

Jerzy: U − V = U + (− V)

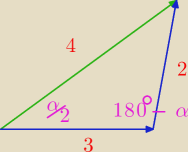
Adamm: jednak źle 4²=3²+2²−2*3*2*cos(180^o−α) 4²=3²+2²+2*3*2*cosα

	1
cosα=
	4

U•V=3/2

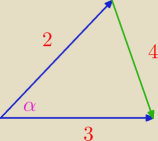
Adamm: jak jest różnica to jest łatwiej, bo korzystasz z twierdzenia Carnota od razu

Adamm: tam nie powinno być α/2, ale mimo wszystko drugi kąt wynosi 180^o−α

Alglin: Czyli w pierwszym przypadku 3/2, a w drugim −20? Piszę o samych iloczynach skalarnych

Adamm: w drugim będzie z plusem

Adamm: i zauważ że tutaj nawet nie ma trójkąta zawsze sprawdzaj czy jest spełniona nierówność a+b≥c gdzie a, b, c to długości wektorów

Alglin: ok mniej wiecej kumam, ide to pocwiczyc, dzieki