równoramienny save: Pokaż że ABC jest równoramienny wtedy i tylko wtedy gdy ³√a−b+³√b−c+³√c−a=0 a,b,c−długosci boków

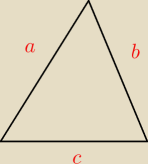
Adamm: załóżmy że trójkąt jest równoramienny oraz a=b wtedy dla b≠c mamy ³√a−b+³√b−c+³√c−a=³√b−c+³√c−a=

	b−c+c−a
=		=
	(b−c)2/3+(b−c)1/3(c−a)1/3+(c−a)2/3

=0 dla b=c mamy ³√a−b+³√b−c+³√c−a=0 trywialnie teraz załóżmy że zachodzi ³√a−b+³√b−c+³√c−a=0 oraz a≠b, b≠c, c≠a

	a−c
3√a−b+3√b−c+3√c−a=		+3√c−a=0
	(a−b)2/3+(a−b)1/3(b−c)1/3+(b−c)2/3

(a−c)2/3
	+1=0
(a−b)2/3+(a−b)1/3(b−c)1/3+(b−c)2/3

ale

(a−c)2/3
	+1>0
(a−b)2/3+(a−b)1/3(b−c)1/3+(b−c)2/3

sprzeczność zatem musi zachodzić co najmniej jedna z równości a=b, b=c, c=a zatem twierdzenie zostało udowodnione w zupełności

Adamm: tam miało być (b−c)^2/3−(b−c)^1/3(c−a)^1/3+(c−a)^2/3 itd.

Adamm: korzystam ze wzoru x³+y³=(x+y)(x²−xy+y²) oraz tego że x²−xy+y²>0 dla (x; y)≠(0; 0) oraz x²−xy+y²=0 dla (x; y)=(0; 0)

jc: x=³√a−b, y=³√b−c, z=³√c−a x³+y³+z³=0 x+y+z=0 (założenie) x³+y³+z³−3xyz=(x+y+z)(x²+y²+z²−xy−yz−zx) (mamy taki wzór) Wniosek: xyz=0, czyli przynajmniej jeden czynnik = 0, czyli a=b lub b=c lub c=a.

Adamm: a czy istnieją wzory analogiczne do x³+y³+z³−3xyz=(x+y+z)(x²+y²+z²−xy−yz−zx) np. dla większych stopni, lub zwiększonej liczby zmiennych

jc: Nie wiem Coś takiego widziałem (x+y+z)⁵−x⁵−y⁵−z⁵ = ... (nie pamiętam)

Adamm: w porządku dziękuję za starania

Adamm: (x+y+z)⁵−x⁵−y⁵−z⁵=5(x+y)(x+z)(y+z)(x²+y²+z²+xy+xz+yz)

Mila: 1) zał. a≠0⋀b≠0⋀c=0 ⋀ a<b<c ⋀³√(a−b)+³√(b−c)+³√c−a=0 a=k*c i k ∊(0,1) b=m*c i m∊(0,1) i k<m a=k* c a−b=k*c−m*c=c*(k−m) b−c=m*c−c=c*(m−1) c−a=c−k*c=c*(1−k) ³√c*(k−m)+³√c*(m−1)+³√c*(1−k)=0⇔ ³√c*(³√(k−m)+³√m−1+³√1−k)=0⇔ ³√k−m+³√m−1=³√k−1 /³ k−m+3*³√(k−m)²*(m−1)+3*³√(k−m)*(m−1)²+m−1=k−1⇔ 3*³√(k−m)²*(m−1)+3*³√(k−m)*(m−1)²=0 sprzeczność m−1<0, k−m<0 z zał. 2) a=b i c≠a i c≠b to ³√a−b+³√b−c+³√c−a=0⇔ ³√a−a+³√a−c+³√c−a=0⇔0=0