 a) Sporzad wykres funkcji g(x)= x|x−1| x∊R
b) Naszkicuj wykres funkcji f(x)= √x|x−1| okreslonej dla tych wartosci x dla ktorych wzor
ma sens
c) Rozwiaz rownanie √x|x−1|= m dla m= 0,5 im=0 25
d) zbadaj w zaleznosci od m liczbe rozwiazan rownania √x|x−1|=m
a) dla x<1 g(x)= x−x2
dla x≥1 g(x)= x2−x
a) juz mam zalatwiony
Teraz b)
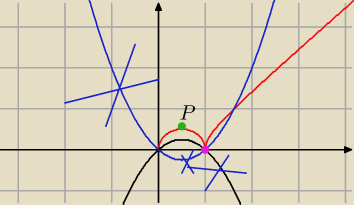
f(x)= √x|x−1| wyszedl mi w programie tutaj (czerwony
Wzor ten jest okreslony dla Df= R+U{0}
Teraz widze ze f(0)= f(1)=0
Teraz muszse obliczyc wspolrzedne punktu P (do d)
jak ?
a) Sporzad wykres funkcji g(x)= x|x−1| x∊R
b) Naszkicuj wykres funkcji f(x)= √x|x−1| okreslonej dla tych wartosci x dla ktorych wzor
ma sens
c) Rozwiaz rownanie √x|x−1|= m dla m= 0,5 im=0 25
d) zbadaj w zaleznosci od m liczbe rozwiazan rownania √x|x−1|=m
a) dla x<1 g(x)= x−x2
dla x≥1 g(x)= x2−x
a) juz mam zalatwiony
Teraz b)
f(x)= √x|x−1| wyszedl mi w programie tutaj (czerwony
Wzor ten jest okreslony dla Df= R+U{0}
Teraz widze ze f(0)= f(1)=0
Teraz muszse obliczyc wspolrzedne punktu P (do d)
jak ?
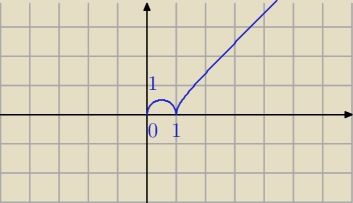 g(x)=√x*|x−1|
D=<0,∞)
|x−1|=x−1 dla x≥1
|x−1|=−x+1 dla x∊<0,1>
g(x)=√x*(−x+1)=√−x2+x dla x∊<0,1>
g(x)=√x*|x−1|
D=<0,∞)
|x−1|=x−1 dla x≥1
|x−1|=−x+1 dla x∊<0,1>
g(x)=√x*(−x+1)=√−x2+x dla x∊<0,1>
| 1 | ||
xw= | ||
| 2 |
| 1 | 1 | |||
g( | )= | |||
| 2 | 2 |
 Drobny blad bo mi wyszlo f(0,5)= 0,25
Drobny blad bo mi wyszlo f(0,5)= 0,25
