Mógłby ktoś rozpisać ? Z góry dziękuje Sophia: Dany jest równoramienny trójkąt prostokątny, którego przeciwprostokątna ma długość 22. Bok ABAB prostokąta ABCDABCD zawiera się w przeciwprostokątnej tego trójkąta,zaś punkty CC i DD należą do przyprostokątnych. Oblicz długości boków prostokąta ABCDABCD wiedząc, że kwadrat długości jego przekątnej ACAC ma wartość najmniejszą z możliwych.

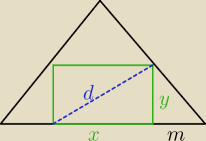
Jerzy: d² = x² + y² ⇔ d = √x² + y²

	22 − x
m =		i y = m
	2

Podstaw do wzoru na d i szukaj minimum funkcji: d(x)

Sophia: Czy to będzie d(18)=28 ?

Sophia: Proszę o odpowiedź Jerzy

Sophia: Mógłby ktoś podać odpowiedź . Bardzo proszę

Sophia: Czy to będzie d(18)=28 ?

Jerzy:

	22 − x
d2 = x2 + (		)2
	2

	22 − x
Wystarczy zatem poszukać minimum funkcji: d(x) = x2 + (		)2
	2

( minimum trójmianu kwadratowego )