całkę potrójną snow: Wykorzystując całkę potrójną obliczyć objętość bryły ograniczonej powierzchniami z=√x²+y² z=0 , x²+y²+4x V: 0≤r≤4cosα −π≤α≤π 0≤z≤x²+y²+4x czy dobrze są opisane granice?

snow: 0≤z≤√x²+y²

snow: ?

jc: −π ≤ α ≤ π 0 ≤ r ≤ 4 cos α 0 ≤ z ≤ r

snow: dlaczego r ogranicza od góry ?

'Leszek: Bryla: przez stozek poprowadzono walec (x−2)² + y² = 4 Czyli obszar D : 0 ≤ r ≤ 4 cos φ −π/2 ≤ φ ≤ π/2 0 ≤ z ≤ √x² + y² J = r V = ∫ ∫ ∫ dz dx dy = ∫ ∫ √x² + y² dx dy = ∫ r² dr ∫ dφ = ........

snow: no to tak jak ja zrobiłem ale dlaczego u ciebie jest fi od −π/2 do π/2? kolo jest przesunięte w lewo a nie w prawo więc powinna być 2 i 3 ćwiartka a nie 1 i 4 ,choć to chyba na to samo wyjdzie ?

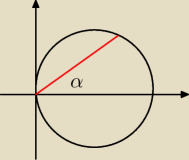
jc: Ma być [−π/2,π/2]. W treści jest coś nie tak. x²+y²+4x ? Czy miało być x²+y² ≤ 4x?

snow: https://scr.hu/A7qP4V też mi się coś tutaj nie zgadzało bo ten stożek nie ogranicza nic od góry czy od dołu więc chyba błąd w zadaniu?

snow: https://www.wolframalpha.com/input/?i=x%5E2%2By%5E2%2B4x%3D0 no i równanie okręgu ,nie wiem dlaczego po prawej to rysujecie

'Leszek: Drodzy uczniowie i studenci piszcie dokladnie tresci zadan , matematyka i fizyka to dziedziny nauk scislych , wiec scislosc , logicznosc i precyzja to podstawa , w przeciwnym razie to sa nieporozumienia i strata czasu ! ! Jezeli x² +y² + 4x = 0 ⇔ (x+2)² + y² = 4 , czyli π/2 ≤ φ ≤ 3π/2

jc: Dla wyniku nie ma to znaczenia, czy po prawej, po lewej, u góry, ...