Pomocy
xyz: 2.Dany jest trójkąt prostokątny równoramienny o przeciwprostokątnej AB,gdzie
A(−5,−3),B(−5,5).Oblicz pole koła wpisanego w ten trójkąt.
4 lip 19:59
xyz: z rysunkiem jak można
4 lip 20:00
xyz: proszę
4 lip 20:01
powrócony z otchłani:
Trojkat prostokatny rownoramienny to nic innego jak polowa kwadratu. Pole trojkata = a2/4
gdzie a = dlugosc przeciwprostokatnej
Albo jak wolisz. a = dlugosc przeciwprostokatnej , b = dlugosc przyprostokatnej
Z tw. Pitagorasa:
b2 = a2/2
P = b2/2 = a2/4
4 lip 20:03
xyz: dziękuje
4 lip 20:04
powrócony z otchłani:
Aaa ... pole kola
r = b − (a/2)
I liczysz pole trojkata
4 lip 20:05
5-latek:
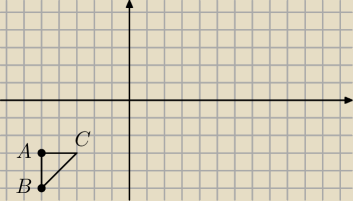
Skoro trojkat ma byc rownoramienny to dlugosc odcinka AB musi byc rowna dlugosci odcinka AC
Z rysunku masz ze wspolrzedne punktu C=(−3,3)
LIcz dlugosc odcinka AB =AC
to dlugosc BC (przeciwprostokatnej wynosi (policz
Wzor
P= p*r
gdzie P to pole trojkata
p− polowa obwodu
r promien kola wpisanego w trojkat
Jest jeszce drugi wzor na r (ale w tej chwili go nie pamietam ) w zaleznoosci o dlugosci bokow
4 lip 20:07
powrócony z otchłani: 5−latek
Zle zaznaczyles punkt B
4 lip 20:12
xyz: to one nie są równe
4 lip 20:14
xyz: ?
4 lip 20:16
5-latek:
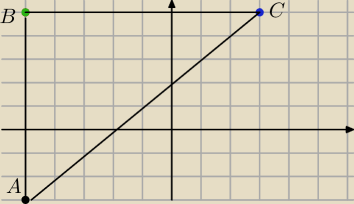
No oczywiscie (nie wiem dlaczego zobaczylem (−5,−5) zamiast (−5 5) .
Skupie sie na swoich zadaniach jednak .
4 lip 20:16
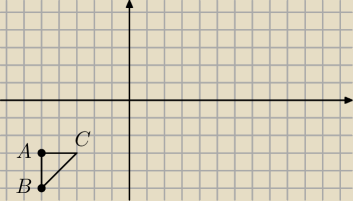 Skoro trojkat ma byc rownoramienny to dlugosc odcinka AB musi byc rowna dlugosci odcinka AC
Z rysunku masz ze wspolrzedne punktu C=(−3,3)
LIcz dlugosc odcinka AB =AC
to dlugosc BC (przeciwprostokatnej wynosi (policz
Wzor
P= p*r
gdzie P to pole trojkata
p− polowa obwodu
r promien kola wpisanego w trojkat
Jest jeszce drugi wzor na r (ale w tej chwili go nie pamietam ) w zaleznoosci o dlugosci bokow
Skoro trojkat ma byc rownoramienny to dlugosc odcinka AB musi byc rowna dlugosci odcinka AC
Z rysunku masz ze wspolrzedne punktu C=(−3,3)
LIcz dlugosc odcinka AB =AC
to dlugosc BC (przeciwprostokatnej wynosi (policz
Wzor
P= p*r
gdzie P to pole trojkata
p− polowa obwodu
r promien kola wpisanego w trojkat
Jest jeszce drugi wzor na r (ale w tej chwili go nie pamietam ) w zaleznoosci o dlugosci bokow
 No oczywiscie (nie wiem dlaczego zobaczylem (−5,−5) zamiast (−5 5) .
Skupie sie na swoich zadaniach jednak .
No oczywiscie (nie wiem dlaczego zobaczylem (−5,−5) zamiast (−5 5) .
Skupie sie na swoich zadaniach jednak .