Proszę o ponowną pomoc :) Sophia: Jednym z miejsc zerowych funkcji F(x)= x³+bx²−13x−10/x+1 jest 5 a) znajdź pozostałe miejsca zerowe funkcji b) wyznacz przedziały monotoniczności funkcji f wyszło mi : b=2 zał: x≠−1 x³+2x²−13x−10/x+1 teraz muszę rozłożyć ten licznik ?

Sophia: tylko ,ze szukam pierwiastków a ich nie ma w liczniku

Sophia: pomocy

Jerzy: Źle policzone b.

Sophia: b=−2 ?

kochanus_niepospolitus: teraz dobrze

Jerzy: Tak.

Sophia: wyszło mi : (x+2)(x−5)(x+1)=0 f(x)>0⇔x∊(−2;1)∪<5;∞) f(x)=0 ⇔ x=−2 lub x=5 lub x=−1 f(x)<0 ⇔x∊(−∞;−2) ∪(−1;5) Dobrze ?

Sophia: x≠−1

Sophia: czyli tam odpada x=−1

Jerzy: Masz zbadać monotoniczność funkcji, a nie samego licznika.

Sophia: f(x)>0⇔x∊(−∞.2) ∪ (5;∞) f(x)=0 ⇔ x=−2 lub x=5 f(x)<0 ⇔ x∊(−2;5)

Sophia: Dobrze ?

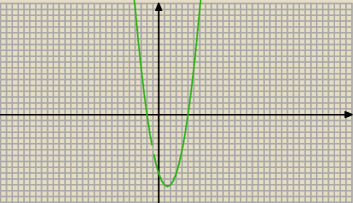
Jerzy: Monotoniczność , czyli przedziały w których rośnie, a w których maleje.

Sophia: tzn ,że źle ?

Jerzy: Źle, bo to nie jest odpowiedź do podpunktu b) W jakim przedziale ta funkcja maleje ? W jakim przedziale ta funkcja rośnie ?

Sophia: chodzi Ci ,że f(x)↘w zbiorze (−∞;2) oraz (5;∞) itd?

Sophia: znaczy ↖ rośnie tam powinno być

Jerzy: Patrz na wykres tej funkcji (10:40) i określ jej monotoniczność.

Sophia: aa f(x)↘ w zbiorze (−∞ ; − 12 1/4) f(x)↗ w zbiorze (−12 1/4 ; ∞) mam to z programu

Jerzy: A co to ma być: − 12 1/4

Sophia: znaczy 15 tam powinno być ,ale już wiem o co chodzi

Jerzy: Jakie 15 ?

Sophia: −130/40

Jerzy: Zosiu ... ile wynosi odcięta wierzchołka tej paraboli ?

Sophia: 3/2

Sophia: jak policzyłam f(3/2)=−13/4 ,ale patrzymy na x

Jerzy:

	3
Nareszcie ... zamiast tego 12 1/4 powpisuj		i po temacie ( Twój post 10:59)
	2

Jerzy: No pewnie ,że na x , a nie na y !

Sophia: dziękuje bardzo za pomoc

piotr: f(x)↘ w zbiorze (−∞ ; −1)∪(−1; 3/2) f(x)↗ w zbiorze (3/2 ; +∞)

Jerzy: No przecież .... x = −1 nie należy do dziedziny