Proszę o pomoc bardzo :) Sophia: Wykaż ,że funkcja g(x)=x+9/x dla dodatnich argumentów przyjmuje wartości nie mniejsze od 6/ Mogłby ktoś wytłumaczyć ? Skoro to jest hiperbola to jak nie mniejsze od 6 , ona nie dąży do nieskończoności?

Jerzy: Poszukaj ekstrema lokalne tej funkcji.

piotr: x+9/x≥6 ⇒

(x − 3)2
	≥0
x

⇒ x>0 rozwiązanie powyższego zawiera się w ℛ⁺, cnd.

piotr: ! odwrotnie ℛ⁺ zawiera się w zbiorze rozwiązań powyższego równania i z tego wynika, że "dla dodatnich argumentów przyjmuje wartości nie mniejsze od 6" cnd.

Sophia: dziękuje bardzo a jak by to wyglądało z ekstremum ?

Jerzy:

	9
f'(x) = 1 −
	x2

f'(x) = 0 ⇔ x = −3 lun x = 3 Dla x = 3 masz minimum lokalne: f_min = 6

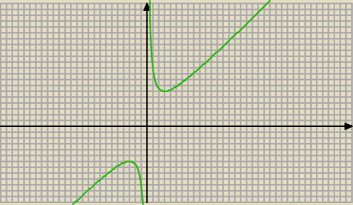
Jerzy: A to wykres.

Sophia: aby narysować ten wykres wziąłeś f(x)=1−9/x² ?

Jerzy:

	9
Nie , to jest wykres funkcji wyjściowej: f(x) = x +
	x

Sophia: już rozumiem dziękuje bardzo