ekstrema lokalne ruber: Witam, czy jak funkcja nie jest ciągła w jakimś punkcie to może mieć w nim maksimum lub minimum lokalne?

Adamm: tak

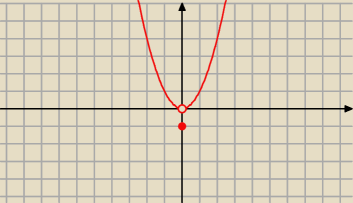
Adamm: przykład takiej funkcji f(x)=x² dla x≠0 −1 dla x=0 funkcja nie jest ciągła dla x=0 ale mimo to przyjmuje tam swoje minimum lokalne

ruber: czyli jak np. byłaby taka sytuacja, że funkcja w danym punkcie ciągła nie jest (czyli pochodna tez nie istnieje w tym punkcie ale ten punkt należy do dziedziny naszej funkcji i pochodna ,,na lewo'' od tego punktu ma inny znak niż pochodna ,,na prawo '' od tego punktu to funkcja ma minimum lub maksimum lokalne?

Jerzy: Pochodna, to narzędzie do liczenia ekstremów. Funkcja f(x) = |x| nie posiada pochodnej w x = 0 , a ma tam minimum globalne.

Adamm: tak

Adamm: nie, stój nie musi mieć

ruber: okej dziękuję za pomoc

ruber: no czyli nie musi mieć pochodnej i nie musi być ciągła w danym punkcie żeby ekstremum było...

Jerzy: Tak.

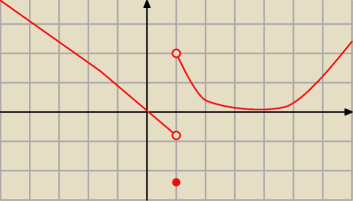
kochanus_niepospolitus: jeżeli funkcja nie jest ciągła w okolicy x_o to nie istotny znak pochodnej 'na prawo' i 'na lewo' od punktu x₀ przykład na rysunku. Tutaj funkcja posiada minimum lokalne w punkcie x₀=1 mimo, że pochodna dla x<x₀ oraz x>x₀ (w okolicy punktu x_o) jest tego samego znaku

Adamm: to zależy czasami jest istotny

ruber: okej dziekuję wszystkim raz jeszcze