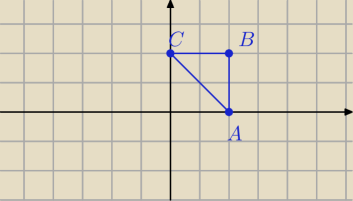
Green student: Twierdzenie Greena mam taki trójkąt zorientowany dodatnio A=(2,0) B=(2,2) C=(0,2) i nie wiem czy robię dobrze czyli to będzie całka 2 2 ∫dx ∫dy 0 −x+2

student: ?

Adamm: liczysz całkę po czym po 1? to tak

Adamm: pomyłka, nie ważne powiedz po czym liczysz całkę

student: Mam taką całkę ∮xy²dx+2x²ydy No i ustalam obszar całkowania, tylko nie wiem czy dobrze to zrobiłem. 2 2 ∫dx∫(4xy−2yx)dy 0 −x+2

Adamm: dobrze

g: Co właściwie oznacza taki napis ∮xy²dx+2x²ydy

student: A co jeśli by ten trójkąt był zorientowany ujemnie?

Adamm: dodajesz minusa i masz zorientowanego dodatnio g, całkę krzywoliniową dla której zachodzi twierdzenie Green'a

student: Adamm masz jeszcze chwilę?

Adamm: o co chodzi

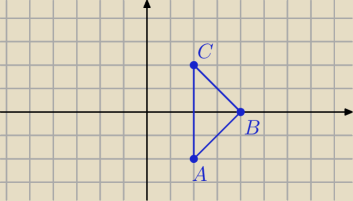
student: A np taki obszar A=(2,−2) B=(4,0) C=(2,2) 4 −x+4 ∫dx∫(.......)dy 2 x−4

Adamm: tak

student: Ok, dzięki.

g: nadal nie rozumiem. czy ∮xy²dx+2x²ydy = ∮xy²dx + ∮2x²ydy

Adamm: aha czyli zwykłe czepialstwo

g: naprawdę nie rozumiem. jeśli nie umiesz wyjaśnić, to może ktoś inny....