proszę o rozwiązanie
Anna: Przekątne sąsiednich ścian bocznych prostopadłościanu wychodzące z jednego wierzchołka
| | π | |
tworzą z jego podstawą kąty o miarach |
| i α Cosinus kąta między tymi przekątnymi |
| | 3 | |
| | √6 | |
jest równy |
| wyznacz miarę kąta α |
| | 4 | |
2 lip 13:13
Mila:
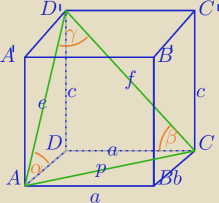
α=?
1)
W ΔD'DC:
p
2=a
2+b
2
e
2=b
2+c
2=b
2+3a
2
2)
W ΔACD' z tw. cosinusów:
p
2=e
2+f
2−2e*f*cosγ
| | √6 | |
a2+b2=b2+3a2+4a2−2*√b2+3a2*2a* |
| |
| | 4 | |
6a
2=a*
√b2+3a2*
√6 ⇔6a=
√6*
√b2+3a2 /
2
36a
2=6b
2+18a
2 ⇔6b
2=18a
2
b
2=3a
2 ⇔
b=√3a
3)
W ΔADD':
========
2 lip 15:51
'Leszek: @Mila , zle masz zaznaczone katy α i β !
powinno byc : α = kat D'AC , β = kat D'CA , w tresci napisane jest katy z podstawa ,a u Ciebie
sa zaznaczone katy z krawedziami podstawy !
2 lip 16:15
Mila:
Rzutem pkt. A na podstawę ABCD jest punkt A,
rzutem prostokątnym pkt. D' na podstawę ABCD jest punkt D.
2 lip 16:31
Anna: dziękuję bardzo
2 lip 17:25
Mila:

2 lip 22:05

