Koniec wielomianow 5-latek: Ostatnie ze zbioru zadanie z wielomianow Wiemy z e dla x=x₁ wielomian W(x) ma minimum dla x=x₂ wielomian W(x) ma amksimum i W(x₁)>W(x₂) Ktorego co anjmniej stopnia jest wielomian W(x)? Odpowiedz przedstaw na wykresie

Adamm: piątego

5-latek: Dobrze Adamm Dlaczego tak?

5-latek: Wiem ze klania sie w pas teoria ale zadania z pochodnych i calek mam na koncu zbioru

Adamm: jak ma dwa ekstrema, i x₁<x₂ (odpowiednio x₁>x₂) to musi być W(x₁)<W(x₂) (W(x₁)>W(x₂)) ponieważ ekstrema to punkty w których zmienia się monotoniczność wielomianu a jeśli najpierw ma minimum, to funkcja musiała wcześniej maleć, itd. więc musi mieć co najmniej 3 jeśli ma 3 to podobnie, minima są przy maksimach, i nie ma innej możliwości jak to żeby W(x₁)<W(x₂) więc musi mieć co najmniej 4, czyli wielomian jest co najmniej stopnia 5, a nie trudno sobie taki wyobrazić

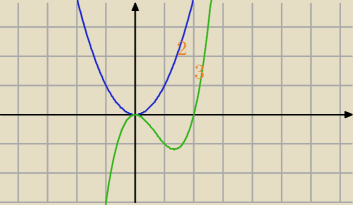
Mila: Myśl dalej.

5-latek: dzieki za pomoc . Trzeba docenic

5-latek: Dobry wieczor Milu Pozdrawiam Moze jutro sie wybiore na Lato Kwiatow do Otmuchowa Ma byc Doda .

Mila: Doda −Fleur. ? Miłej imprezy

5-latek: