funkcja analityczna Anka.: Punkty A(1,7), B(−5,1), C(7, −5) są wierzchołkami trójkąta ABC. Oblicz odległość między środkiem okręgu opisanego na tym trójkącie a środkiem ciężkości tego trójąta. Proszę o rozwiązanie, bo leże z tego działu, a potrzebuje tego na jutro

ula: pomogę ci, tylko tu jest strasznie dużo pisania

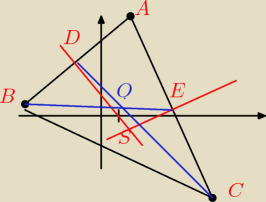
ula: środkowe Δprzecinają się w środku ciężkości (na rysunku punkt O)

	yA+yB+yC
O=(U{xA+xB+xC}{3;		)
	3

O=(0;3) żeby wyliczyć punkt S (przecięcie się symetralnych boków Δ) trzeba ustalić proste SD i SE (są prostopadłe do BA i AC) obliczmy najpierw punkt D − jest to środek odcinka BA

	xB+xA		yB+yA
czyli D=(		;		)
	2		2

D=(−2,4) punkt E

	xA+xC		yA+yC
E=(		;		)
	2		2

E=(4;1) współczynnik kierunkowy prostej BA

	yB−yA
a1=		=1
	xB−xA

współczynnik prostej DS prostopadłej do BA a2=−¹_a1=−1 prosta DS y=ax+b przechodzi przez D 4=−1*(−2)+b → b=2 y=−x+2 na tej samej zasadzie oblicz prostą SE

	yC−yA
współczynnik kierunkowy pr AC a3=		=−4
	xC−xA

współ pr SE a4=⁻¹_a3=¹₄ prosta SE y=¹₄x+b przechodzi przez punkt E(4,1) 1=¹₄*4+b →b=0 y=¹₄x punkt S to { y=−x+2 {y=¹₄ x=⁷₄ odległość punktu S od punktu O to wzór d=√(x_S−x_O)²+(y_S−y_O)² podstaw