Równanie stycznej do funkcji f(x)=1-p{4-x^2} w punkcie przec. z OY smazony: Witam, mam takie zadanie: Napisz równanie stycznej do wykresu funkcji f(x)=1−√4−x² w punkcie przecięcia się wykresu z osią OY. Tak więc chciałbym się zapytać czy dobrze rozumuję? Robię to tak: Najpierw obliczam wartość współrzędnych punktu z wykresu w/w funkcji przecięcia z osią OY, czyli: f(x)=1−√4−x² f(0)=1−√4−0² f(0)=−1 czyli: x₀=0 (bo w końcu tak trzeba było podstawić) i y₀=−1 (bo tyle wyszło i jest to wartość funkcji w punkcie x₀) Zatem ten punkt ma współrzędne P=(0,−1). Następnie liczę pochodną z funkcji. Po wyliczeniach wychodzi f'(x)=−x/√4−x² Następnie wartość pochodnej w punkcie przecięcia z OY czyli w x₀ czyli to jest: f'(x₀)= −0/√4−0²=0 Zatem po podstawieniu do wzoru na styczną y−y₀=f'(x₀)(x−x₀), jeżeli wartość f'(x₀)=0 to prawa strona się zeruje i wychodzi y=y₀ y=−1 Rozumiem że wstawiam tu wcześniej obliczone y₀

smazony: Dziękuję bardzo za odpowiedź, nie byłem pewny czy dobrze kumam w czym rzecz

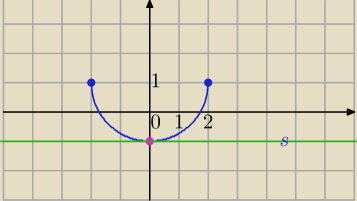Mila: y=1−√4−x² D=<−2,2> s: y=−1