Proszę znaleźć objętość przestrzeni zamiecionej przez obrót wokół osi OY Hubert.: Proszę znaleźć objętość przestrzeni zamiecionej przez obrót wokół osi OY obszaru ograniczonego krzywymi: y = 2 − x² i y = 1. Witam, mam problem z tym zadaniem. Normalnym procesem byłoby znalezienie punktów przecięcia, które potem stałyby się granicami całkowania i skorzystałbym ze wzoru na objętość. Tutaj sytuacja ma się pewnie podobnie, nie wiem jednak jak konkretnie zareagować na obrót wokół osi OY, muszę wyliczyć z tych równań x?

Jerzy: Musisz po prostu odwrócić układ współrzędnych.

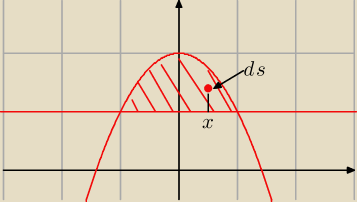
g: Każdy element tej powierzchni ds dodaje do objętości dv = 2π x ds.

g: poprawka: dv = 2π |x| ds V = ∫₋₁¹ ∫₁^2−x2 2π |x| dy dx = 2π ∫₋₁¹ (1−x²)*|x| dx = π ∫₀¹ (1−x²)*x dx

g: znowu poprawka: wystarczy obracać tylko połówkę tej powierzchni. V = 2π ∫₀¹ (1−x²)*x dx