szybka pomoc - studia patryk: 1. Metodą przewidywań rozwiązać równanie różniczkowe liniowe : y'''−2y''=12x − e^x 2. Wyznaczyć całkę ogólną równania różniczkowego (1+y)dx = (1−y)dy 3. Obliczyć całkę podwójną {{ (y/x) dxdy w obszarze D opisanym warunkami : x² + y² <= 1 , y>=0 , y<=x

kochanus_niepospolitus: 1) Przewiduję, że y = A + Bx + Cx² − x³ + De^2x + e^x

Mariusz:

	1−y
dx=		dy
	1+y

	−1−y+2
dx=		dy
	1+y

	2
dx=(−1+		)dy
	1+y

i całkujesz obustronnie

patryk: kurczę, pomyłka tam powinno być: (1+y)dx = (1−x)dy

powrócony z otchłani: No to masz: dx/(1+x) = dy/(1−y) Czy Ty chodziles w ogole na zajecia?

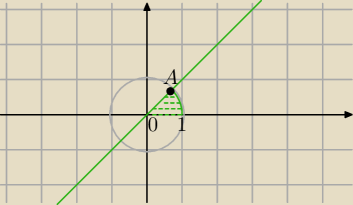
Mila: Obliczyć całkę podwójną: ∫∫ (y/x) dxdy w obszarze D opisanym warunkami : x² + y² ≤ 1 , y≥0 , y≤x x=r cosφ y=r sinφ r²*cos²φ+r²*sinφ≤1⇔

	π
r2≤1 i r sinφ≥0 i r sinφ≤r cosφ⇔φ∊<0,		> i r∊<0,1>
	4

	sinφ
0∫1[0∫π/4		dφ ]r dr=
	cosφ

	√2
=0∫1[−ln|cosφ|])0π/4] r dr=0∫1[−ln(		)+ln1] *rdr=
	2

	1		ln(√2)		ln(2)
=ln(√2)0∫1rdr=ln(√2)[		r2]01=		=
	2		2		4