Uzasadnić arcsin1+x=1 stephen: Mam za zadanie uzasadnić, że arcsinx+x=1 w przedziale (0,1) ma dokładnie 1 rozwiązanie. Koś coś?

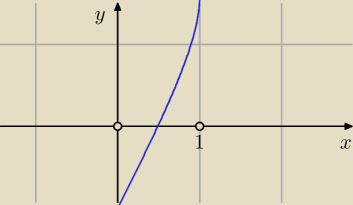
Janek191: f(x) = arcsin x + x − 1

	1
f '(x) =		+ 1 > 0 dla x ∊ ( 0, 1)
	√1 − x2

więc f jest rosnąca w ( 0, 1)

stephen: Dzięki!

Adamm: f(x) jest rosnąca a ponieważ jest ciągła, oraz f(0)=−1<0, f(1)=π/2>0 to istnieje co najmniej jeden pierwiastek x taki że x∊(0;1) no ale jest rosnąca, więc więcej niż jeden być nie może