matematykaszkolna.pl
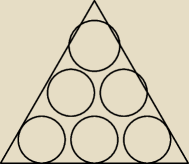
geometria Adamm: rysunek
 n(n+1) 
mamy dane
okręgów o równych promieniach wpisanych
 2 
w trójkąt równoboczny o boku a, tak jak na rysunku (dla n=3) ile wynosi promień?
24 cze 23:59
jc:
 a 
r =
 2n−2+√3 
25 cze 00:15
Adamm: n=1
 a 
r=
 √3 
wzór nie zachodzi
25 cze 00:16
jc: No to pewnie
 a 
r =
 2(n−1+√3) 
25 cze 00:19
jc: Dobranoc emotka
25 cze 00:20
Adamm: dobranoc
25 cze 00:20
Adamm: zadanie nadal aktualne, proszę się nie krępować
25 cze 00:41
Saizou : a mnie wyszło
 a 
r=
 2√3−1+n 
25 cze 18:01
g: Drugie rozwiązanie jc jest poprawne. @Saizou, musi być 2*(n−1), bo środki okręgów oddalone są o 2*r.
25 cze 18:04
Saizou : zaraz sprawdzę rachunki
25 cze 18:05
Saizou : faktycznie walnąłem gafę obliczeniową
25 cze 18:08
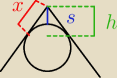
Adamm: rysunekok, no to tak wysokość bez s wynosi 2r+√3(n−1)r 2x2−2x2cos60o=2r2−2r2cos120o x=√3r
 x√3 3 
h=
=
r
 2 2 
 1 
h+
r=s+r
 2 
s=r H − wysokość całego H=3r+√3(n−1)r
 2√3 
a=
*(3r+√3(n−1)r)=2√3r+2(n−1)r
 3 
 a 
r=
 2√3+2(n−1) 
25 cze 18:55