Pole figury ograniczonej krzywymy matematyk: Witam, potrzebuję obliczyć pole figury ograniczonej krzywymi: y=x², y=4x², y=16. Narysowalem wykres i wiem jaki to obszar lecz zastanawiam się jak podstawic granice do całki. X zmienia się od − 4 do 4, a y od x² do 16? W takim razie będzie co całka ∫ od − 4 do 4 z (16−x²)?

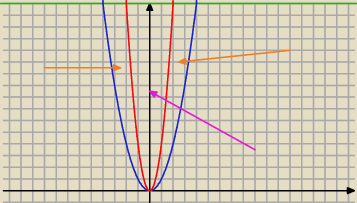
po prostu Michał: chodzi o obszary oznaczone strzalka brazowa czy ten w srodku oznaczony czerwona

kochanus_niepospolitus: Jak już to mamy: ∫₋₄⁴ (16−x²) dx − ∫₋₂² (16 − 4x²) dx

kochanus_niepospolitus: Michał ... z pewnością brązowa ... do fioletowego obszaru zbyteczna byłaby informacja o funkcji f(x) = 4x²

: a co na to autor autor

matematyk: W treści zadania nie ma żadnych nierówności więc sam założyłem że chodzi o tą zaznaczona brązowym strzałkami.

matematyk: @kochanus Dziękuję bardzo, tak też mi się wydawało

hehesz: ja bym policzyl w ten sposob: 2 4 2 [ ∫ 3x² dx + ∫ (16−x²) dx] 0 2

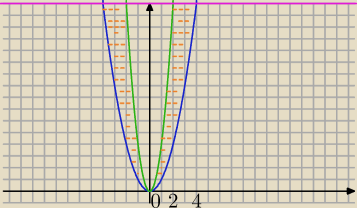
Mila: Obszar normalny względem OY y≥0 y=x²⇔x=√y

	√y
y=4x2⇔x=
	2

	√y		2
P=2*0∫16(√y−		dy=0∫16y1/2 dy=[		y3/2]016=
	2		3

	128
=
	3