wyznacz przedziały monotonicznośći i ekstrema lokalne funkcji arek: czesc, jestem studentem 1 roku i mam pewien problem z zadaniem wyznacz przedziały monotonicznośći i ekstrema lokalne funkcji f(x) = (−x² + 4) / 2x wynik mi wychodzi ze funkcja jest malejaca do −0.354 i rosnaca do 1.365

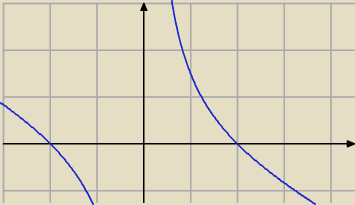
Janek191: Df = ℛ \ { 0}

	−2 x*2 x − (−x2 + 4)*2		− 4 x2 + 2 x2 − 8
f '(x) =		=		=
	4 x2		4 x2

	− 2 x2 − 8		− x2 − 4
=		=		< 0 dla x ∊ Df
	4 x2		2 x2

więc funkcja f maleje w swojej dziedzinie ; ( − ∞, 0) , ( 0, +∞)

arek: ok wiec tutaj nie ma ekstremów ? czy te ekstrema to poprostu 0 ?

Janek191: Nie ma ekstremum.

kochanus_niepospolitus: studencie ... naucz się aby nie podawać wartości po przecinku tylko w postaci ułamka nieskracalnego