probal Benny: Rzucono niezależnie 16 razy symetryczną monetą. Obliczyć prawdopodobieństwo tego, że uzyskano co najwyżej 5 serii, jeśli wiadomo, że uzyskano 10 orłów i 6 reszek. Serią nazywamy ciąg elementów jednego typu, przed i za którym występuje element drugiego typu. Na przykład aaabbbbaabbbba jest 5 serii, 3 typu a i 2 typu b.

Adamm: x₁+x₂+x₃=10, x₁+x₂=6, x_i≥0

10+3−1 10		6+2−1 6
	*

x₁+x₂=10, x₁+x₂+x₃=6, x_i≥0

10+2−1 10		6+3−1 6
	*

	10+3−1 10   6+2−1 6   10+2−1 10   6+3−1 6   * + *		5
P=		=
	16 10		52

a przynajmniej tak mi się wydaje

Adamm: nie, co najwyżej to by było dokładnie 5 x₁+x₂=10, x₁+x₂=6, x_i≥0 x₁=10, x₁+x₂=6 x₁+x₂=10, x₁=6

	12 10   7 6   11 10   8 8   11 10   7 6   7 6   11 10   * + * +2* * + + +2
P=		=
	16 10

	118
=
	1001

Adamm: nie, wróć to jeszcze by było inaczej, bo jak x_i=0 to już nie mamy serii

Benny: To któreś jest ok?

Adamm: żadne, ale jeśli zastosujesz to co w poście 20:53, ale dla x_i≥1, powinno być ok

Pytający: 2 serie: 2 sposoby 3 serie: o₁r₁o₂ ⋁ r₁o₁r₂ ((o₁+1)+(o₂+1)=10 ∧ r₁=6) ∨ ((r₁+1)+(r₂+1)=6 ∧ o₁=10), o_i≥0, r_i≥0

8+2−1 8		4+2−1 4
	*1+		*1=14 sposobów

4 serie: o₁r₁o₂r₂ ⋁ r₁o₁r₂o₂ ((o₁+1)+(o₂+1)=10 ∧ (r₁+1)+(r₂+1)=6) ∨ ((o₁+1)+(o₂+1)=10 ∧ (r₁+1)+(r₂+1)=6), o_i≥0, r_i≥0

	8+2−1 8		4+2−1 4
2*		*		=90 sposobów

5 serii: o₁r₁o₂r₂o₃ ⋁ r₁o₁r₂o₂r₃ ((o₁+1)+(o₂+1)+(o₃+1)=10 ∧ (r₁+1)+(r₂+1)=6) ∨ ((o₁+1)+(o₂+1)=10 ∧ (r₁+1)+(r₂+1)+(r₃+1)=6), o_i≥0, r_i≥0

7+3−1 7		4+2−1 4		8+2−1 8		3+3−1 3
	*		+		*		=270 sposobów

	2+14+90+270		47
P=		=
	16 10		1001

Inaczej policzona liczba sposobów: − 6 reszek możemy wstawić jako 1 serię pośród 10 orłów na 11 sposobów (tworząc łącznie 2 serie gdy wstawimy z brzegu lub 3 serie wstawiając gdzieś po środku) − 6 reszek możemy wstawić jako 2 serie pośród 10 orłów na 5*55 sposobów (tworząc łącznie 3, 4 lub 5 serii)(reszki ustawiamy w 2 serie na 5 sposobów, te 2 serie wstawiamy na 10+9+...+1=55 sposobów) − 6 reszek możemy wstawić jako 3 serie pośród 10 orłów (tak, aby łącznie było 5 serii − pierwsza seria przed orły, druga po środku, trzecia za orłami) na 10*9 sposobów (reszki ustawiamy w 3 serie na 10 sposobów, środkową serię wstawiamy na 9 możliwych pozycji)

	11+5*55+9*10		47
P=		=
	16 10		1001

Mila: Hej ! Pytający Rysuję kratownicę, ale mam mętlik w rachunkach.

Benny: Dzięki

Pytający: Hej, Milu! (tak na dzień dobry ) Dla kraty (6x10) rachunki tak bym rozpisał: // [zaczynając w górę]+[zaczynając w prawo] − 2 serie (1 zakręt) − [1]+[1]=2 przypadki − 3 serie (2 zakręty) − [5]+[9]=14 przypadków − 4 serie (3 zakręty) − [5*9]+[5*9]=90 przypadków

	5 2		9 2
− 5 serii (4 zakręty) − [		*9]+[		*5]=270 przypadków

I proszę bardzo, Benny.

Mila: Dzień dobry! Dziękuję, kawka była rano . Kratę wpiszę do swoich notatek. Miłego popołudnia.

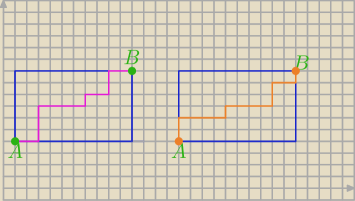
Mila: Z kratownicą dla 7 serii. B− uzyskano dokładnie 7 serii. x₁+x₂+x₃+x₄=10−4 i y₁+y₂+y₃=6−3

6+4−1 4−1		3+3−1 3−1		9 3		5 2
	*		=		*		=840

lub x₁+x₂+x₃=10−3 i y₁+y₂+y₃+y₄=6−4

7+3−1 3−1		2+4−1 4−1		9 2		5 3
	*		=		*		=36*10=360

	840+360		1200		150
P(B)=		=		=
	8008		8008		1001

Mila: To dla Bennego.

Benny: Jak to działa?

Mila: Pierwsza kratka prezentuje rozwiązanie: OORRROOOOROORROO − masz 7 serii 4 serie O: x₁,x₂,x₃,x₄ 3 serie R: y₁,y₂,y₃ x₁+x₂+x₃+x₄=10 i y₁+y₂+y₃=6 szukana liczba rozwiązań całkowitych dodatnich⇔

	10−1 4−1		9 3		6−1 3−1		5 2
szukana liczba rozwiązań odpowiednio:		=		=84 i		=		=10

( albo tak jak liczyłam wcześniej− to jasne?) Liczba możliwości: 84*10=840 Dalej już wiesz?

Benny: Przejrzę to

Benny: Dzięki

Mila: Zrozumiałeś?

kptadrian: nie xD

Benny: Witaj Milu, czy to są wszystkie drogi, które prowadzą do B?

Benny: Oczywiście takie drogi, które mają co najwyżej 5 pionowych kresek?

Mila: 27 czerwca 15:16 dotyczy innego zadania. Masz tam sposób dla 7 serii . (3serie O i 4serie R ) lub (4serie O i 3 serie R). Twoje zadanie z 23 czerwca rozwiązał Pytający. Nie bardzo wiem, o co ci chodzi.

Benny: Źle spojrzałem i stąd to nieporozumienie. Wydaje mi się że załapałem o co chodzi.

Benny: dla Ciebie

Mila:

daras: ale tylko mu sie tak wydaje