prob janusz: Z odcinka [2,12] wybieramy kolejno po dwie liczby x i y, aż xy > 48. Podać rozkład zmiennej losowej opisującej liczbę losowań. Jakie jest prawdopodobieństwo, że wykonamy nieparzystą liczbę losowań (losowanie to wybór x i y)?

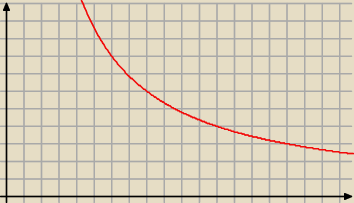
Adamm: mamy prawd. geometryczne prawd. że xy>48 wynosi

	∫412∫48/x12dydx		∫41212−48/xdx
P=		=		=
	(12−2)2		100

	24−12ln3
=		≈0,4326661014
	25

prawd. że wykonamy nieparzystą liczbę losowań:

	P
P+(1−P)2*P+(1−P)4*P+...=		≈0,6380261417
	1−(1−P)2

janusz: mam 2 pytania dlaczego 4≤x≤12 ? i czy mógłbyś wytłumaczyć mi to z nieparzystą liczbą losowań>?

janusz: ok warunek x się zgadza

Adamm: 4≤x≤12 ponieważ nasz obszar mieści się między x=4 a x=12 no nie wiem jak inaczej to wytłumaczyć

48
	=12 dla x=4
x

to jest po prostu granica tego obszaru dla nieparzystej liczby losowań mamy tak albo wygraliśmy z pierwszym razem, dlatego P albo przegraliśmy 2 razy, dlatego (1−P)², i wygraliśmy, dlatego P itd. mamy szereg geometryczny, stosujemy wzór na jego sumę

janusz: dzięki