calka Beorn: Jak to policzyć?

	2
∫		(1−|x|)3
	3

kochanus_niepospolitus: tam masz wartość bezwzględną

kochanus_niepospolitus: Najprościej rozbić całkę na dwa przypadki: x>0 i x<0 dla x=0 nie jest całkowalna

Beorn:

	2		2
czyli mam policzyć całke ∫		(1−x)3 i ∫		(1+x)3 ?
	3		3

kochanus_niepospolitus: Tak ... ewentualnie później korzystasz z funkcji sgn(x) która jest równa: −1 dla x<0 0 dla x=0 1 dla x>0

'Leszek: Tak , ale dopisuj do calki zawsze rozniczke dx (2/3) ∫ (1−x)³ dx = ...... Dla x=0 , (2/3) ∫ (1−0)³ dx = (2/3) x + C

Beorn: właściwie to muszę policzyć oznaczoną https://www.wolframalpha.com/input/?i=integral+2%2F3+(1+-+abs(x))%5E3+for+x+from+-1+to+1 ale wolphram mi pokazuje jedno rozwiązanie więc o co chodzi? nie powinienem dostać 2 jeśli to podziele na 2 przypadki?

'Leszek: Czy cyfry 2 i 3 to sa granice ? jezeli ta to po pierwsze co robi ta kreska ulamkowa ,i calka jest tylko dla x> 0 ? ? ? Napisz poprawnie symbol calki ! !

Beorn: ? przecież poprawnie napisałem nieoznaczoną spójrz na wolphrama tam mam oznaczoną

kochanus_niepospolitus: jeżeli liczysz całkę oznaczoną (i to w dodatku o symetrycznych granicach) to proponuję policzyć:

	2
2∫01		(1−x)3 dx
	3

ponieważ funkcja podcałkowa jest funkcją parzystą

Beorn: no ale co z tą wartościa bezwzględną? mogę sobie ją tak opuścić i liczyć oznaczoną z

	2
		(1−x)3 ?
	3

kochanus_niepospolitus: pamiętaj także że wolframalpha całki oznaczone liczy w inny sposób niż Ty na kartce papieru ... program nie wylicza wtedy funkcji pierwotnej

kochanus_niepospolitus:

	2
Beorn ... funkcja jest PARZYSTA .... dla x>0 funkcja podcałkowa ma postać		(1−x)3
	3

więc całkujesz ją w takiej właśnie postaci ... mnożąc całkę przez 2 ze względu na granice całkowania

kochanus_niepospolitus: Analogiczna sytuacja: ∫₋₁¹ |x³| dx = 2∫₀¹ x³ dx ale także = 2∫₋₁⁰ −x³ dx

Mila:

	2
f(x)=		(1−|x|)
	3

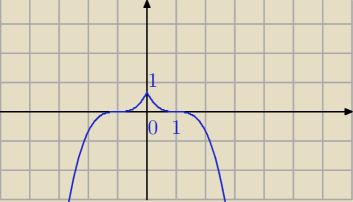
Nie zauważyłam wcześniej wart. bezwzględnej. Przepraszam. f(x) jest parzysta