SPR 1551: Proszę o sprawdzenie kilku zadań oraz pomoc w jednym z nich(ostatnie). 1.Oblicz pochodne cząstkowe f(x,y)=⁷√x⁷−y w (x,y)=(0,0). Tutaj liczyłem z definicji :

df		Δx−0
	= limΔx−>0U{f(x0+Δx,y0}−f(x0,y0)}{Δx} = limΔx−>0		=1
dx		Δx

df		7√−Δy
	=limΔy−>0U{f(x0,y0+Δy}−f(x0,y0)}{Δy} = limΔy−>0		=
dy		Δy

	1
limΔy−>0−(Δy)−67=limΔy−>0−(		)67=−∞
	Δy

Czy zostały wyliczone poprawnie ? 2. Oblicz pole obszaru ograniczonego krzywymi xy=6 oraz x+y = 7

	6
Tutaj wychdzi mi całka ∫(od 1 do 6) [(−x+7)−(		)]dx, ale po rozwiązaniu otrzymuję wynik
	x

17,5−6ln6 co wydaje się dziwnym wynikiem. 3.Ekstremum warunkowe f=xy pod warunkiem φ≡x²+y²−1=0 Rozwiązanie tutaj : http://imgur.com/fPq8cpq 4. I tutaj prosiłbym kogoś o wytłumaczenie mi tego przykładu, ponieważ nie wiem jak go zrobić. Oblicz objętość obszaru ograniczonego : x²+y²=1 x+y+z=4 z=1 Wiem, że trzeba zbudować całkę, ale nie wiem w jaki sposób.

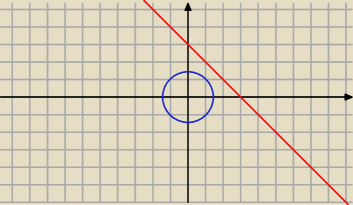
Adamm: 4. tutaj mamy 2 płaszczyzny oraz cylinder 4−x−y≥1 3≥x+y dla naszego obszaru, x²+y²≤1 będziemy mieli 4−x−y≥1, zatem płaszczyzna x+y+z=4 ogranicza z góry, a z=1 ogranicza z dołu zatem mamy 1≤z≤4−x−y oraz x²+y²≤1 x=rcosα, y=rsinα, r∊<0;1>, α∊<0;2π> ∫₀^2π∫₀¹3−rcosα−rsinα dr dα no i pozostało tylko policzyć

kochanus_niepospolitus: f'_x dobrze ... f'_y źle

1551: Co jest źle w f'y ? Mógłbyś policzyć to prawidłowo ?

1551: Dzięki Adam.

Adamm: nie widzę nic złego w f'_y, kochanus się po prostu pomylił

1551: Tak myślałem, na kartce miałem bardziej rozpisane krok po kroku więc zdziwiłem się, że jest błąd. A czy zadanie 2 jest poprawnie rozwiązane ?

1551: Ten wynik jest dosyć dziwny, dlatego budzi moje wątpliwości − być może gdzieś się pomyliłem i nie mogę dostrzec błędu.

1551: ⊂:

1551: Ω

1551: Ω

Adamm: 2. wynik jest ok

1551: Dzięki za pomoc, spokojnej nocy