geometria
Adamm:
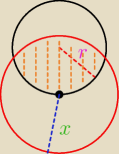
Mamy dane koło o promieniu r. Mamy również dane drugie koło, którego środek leży
na brzegu pierwszego koła. Ile wynosi promień drugiego koła, jeśli wiadomo że
| | 1 | |
pole części wspólnej, to połowa pola pierwszego koła? ( |
| πr2) |
| | 2 | |
21 cze 23:46
jc: Czyżby sławne zadanie o kozie?
22 cze 00:00
Adamm: 
22 cze 00:04
jc: Dobranoc
22 cze 00:09
Adamm: Dobranoc
22 cze 00:11
mat: ciekawe, bo wydaje sie proste a ....
22 cze 00:12
mat: Mam tylko pytanie czy odpowiedź będzie typu ,,aaaa no tak..", czy "masakra"?
22 cze 00:12
Adamm: raczej to drugie
22 cze 00:27
powrócony z otchłani:
Wbrew pozorom nie jest to jakies drastycznie trudne zadanie, ale niestety troche upierdliwe.
Trzeba wyznaczyc wspolrzedne trzech (a tak naprawde to dwoch) punktow:
1) przeciecie sie dwoch okregow,
2) przeciecie sie okregu ze srednica mniejszego okregu bedaca prostopadla do odcinka laczacego
srodki tych okregow,
3) punkt wspolny tejze srednicy z mniejszym okregiem (tego akurat wyliczac nie trzeba)
Dla ulatwienia zakladamy ze srodek jednego z tych okregow lezy na poczatku ukladu
wspolrzednych.
Majac te punkty obliczamy pole trojkata o tych bokach, dodajemy i odejmujemy odpowiednio czesci
pola wykorzystujac wzor na pole wycinka kola i otrzymane pole mnozymy przez 2. Nastepnie
wartosc ta przyrownujemy do czesci duzego kola bedacej ponad srednica malego okregu.
To jest sposob na gimnazjum/liceum. Student natomiast by po prostu policzyl calke nieoznaczona
wywyznaczyl punkty przeciecia sie okregow i podstawil te granice calkowania przyrownujac do
polowy pola okregu.
22 cze 11:36