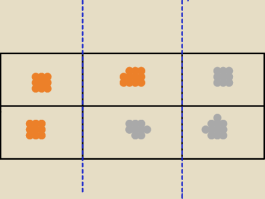
prawdopodobienstwo Beorn: W komodach A, B i C są po dwie szuflady. W każdej szufladzie jest jedna moneta, przy czym w komodzie A są monety złote, w C – srebrne, a w B jest jedna złota i jedna srebrna. Wylosowano komodę, następnie szufladę i znaleziono tam monetę złotą. Jaka jest szansa, że w drugiej szufladzie jest moneta złota? Czy to zadanie można zrobić sobie tak na "logike"? czy trzeba korzystać tutaj z jakiś wzorow i innych komplikacji? P=1/3 ?

Beorn: rysunek sam zrobilem

powrócony z otchłani: Najprosciej ze wzoru na prawdopodobienstwo warunkowe. Na logike to pomysl tak ... masz 3 zlote monety. Wybieramy jedna z nich ... jedna z nich ma 'towarzysza' srebnego, a pozostale dwie sa swoimi towarzyszami. P = ²/₃

Beorn: dlaczego 2/3? przecież jeśli wylosuję złotą monetę to w drugiej szafce musi być albo srebrna albo złota więc 1/3?

Beorn: chociaż nie... jeśli wylosuję złotą to obszar zamyka się do 2 komod więc 1/2?

Pytający: Na logikę, tak jak napisał powrócony mamy 3 możliwości wylosowania szuflady ze złotą monetą (i wiemy, że taką wylosowaliśmy): − jeśli wylosowaliśmy pierwszą szufladę z komody A, to w drugiej szufladzie jest moneta złota − jeśli wylosowaliśmy drugą szufladę z komody A, to w drugiej szufladzie jest moneta złota − jeśli wylosowaliśmy szufladę z monetą złotą z komody B, to w drugiej szufladzie jest moneta srebrna

	2
P=
	3

Wzorkiem: D − wylosowano złotą monetę E − w drugiej szufladzie wylosowanej komody jest złota moneta

	P(E∩D)		1   3		2
P(E|D)=		=		=
	P(D)		1   1   1   + * 3   3   2		3

P(E∩D)=P(wylosowanie komody A) P(D)=P(wylosowanie komody A)+P(wylosowanie komody B)*P(wylosowanie złotej monety z komody B)