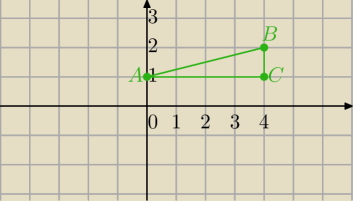
Jak wyliczyć tę całkę po obszarze ? Marlene: Jak wyliczyć tę całkę po obszarze ? ∫∫(2x+3y−1)dxdy D : A(0,1) , B(4,2) , C(4,1)

janek: Obszar można podzielić na 2 obszary normalne : 0≤x≤1

	1
		x+1≤y≤3x+1
	4

oraz 1≤x≤4

	1
		x+1≤y≤5−x
	4

piotr: ∫₀⁴[∫₁^x/4+1(2x+3y−1)dy]dx

piotr: =50/3

Marlene: skąd się wzieła funkcji 3x+1 i 5−x ?

janek: błąd

Marlene:

'Leszek: @Piotr podał CI poprawne rozwiązania , równanie prostej AB : y = x/4 + 1 i dlatego zmienna y zmienia się od y =1 do y = x/4 + 1

janek: rysunek piotra jest dobry i jest to obszar normalny który można przedstawić: 0 ≤ x ≤ 4

	1
1 ≤ y ≤		x + 1
	4

Marlene: nie wychodzi mi coś ta całka: ∫2xdy+∫3ydy−∫dy = 2xy + 3* ^y2₂ − y +c podstawiam i mi wychodzi 17,5

Mila:

	1
AB: y=		x+1
	4

_D∫∫(2x+3y−1)dxdy=₀∫⁴[₁∫^1/4x+1(2x+3y−1)dy]dx=

	3
=0∫4[2xy+		y2−y]11/4x+1 dx=
	2

	1		3		1		1		1		3
=0∫4[		x2+2x+		*(		x2+		x+1)−		x−1−(2x+		−1)] dx=
	2		2		16		2		4		2

	19		1
=0∫4[		x2+		x]dx=
	32		2

	19		1		1		50
=[		*		x3+		x2]04=
	32		3		4		3