geom anal motur: Napisać równanie płaszczyzny przechodzącej przez punkt P(2,1,1)) i prostą: L: 2x−y+z=1 x+y−z=0 Prosiłbym o wytłumaczenie co skąd się bierze itp Pozdrawiam!

jc: Płaszczyzny przechodzące przez L można zapisać równaniem a(2x−y+z−1) + b(x+y−z)=0 Wystarczy teraz tak dobrać a i b, aby punkt P=(2,1,1) leżał na naszej płaszczyźnie a(2*2−1+1−1)+b(2+1−1)=0 3a+2b=0 a=2, b=−3 2(2x−y+z−1)−3(x+y−z)= x − 5y+5z−2 Szukana płaszczyzna x−5y+5z=2

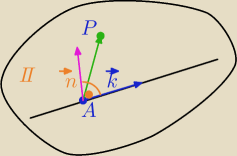
Mila: L: 2x−y+z=1 x+y−z=0 Przyjmuję z jako parametr, z=t, t∊R 2x−y=1−t x+y=t −−−−−−− 3x=1 L: równanie parametryczne prostej L

	1
x=		+0*t
	3

	1
y=−		+t
	3

z=t

	1		1
k→[0,1,1] wektor kierunkowy prostej, A=(		,−		,0)∊L
	3		3

P(2,1,1)

	5		4
AP→[		,		,1]
	3		3

	5		4		1		5		5
n→=[0,1,1] x [		,		,1] = [−		,		,−		] wektor normalny
	3		3		3		3		3

szukanej płaszczyzny π n^→⊥π

	1		5		5
n→= [−		,		,−		] równoległy do wektora n'= [1,−5,5]
	3		3		3

π: 1*(x−2)−5*(y−1)+5*(z−1)=0 x−2−5y+5+5z−5=0 x−5y+5z−2=0