monotonicznosc xyz: zbadaj przebieg zmiennosci funkcji y=ln(x²−1) chodzi mi o monotoniczność i wklęslosc/wypuklosc. moje wyniki różnią się od tych w odpowiedzi, moglby ktos rozwiazac?

kochanus_niepospolitus: to pokaż jak rozwiązujesz ... sprawdzimy

Jerzy: Zacznij od dziedziny i pochodnej.

xyz: dz;=: (−∞,−1)∪(1,∞) y'=2x/(x²−1) przyrównuję do zera , wychodzi, że x=0 funkcja maleje od (−inf,−1)∪(−1,0) funkcja rosnie (0,1)∪(1,inf) y''=−2x²−2/(x²−1)² przyrównuję do zera, wychodzi mi −2x²−2=0 ssprzecznosc, brak rozwiazan, więc funkcja jest ∪ od (−inf,−1) suma (1,inf) jednak w odpowiedziach jest inaczej, nie jest wziety pod uwage ten przedział (−1,0) (chodzi mi o tabelke, w tabelce nie ma 0) ii rózni się wklęsłość bo w odpowiedziach jest, że od (1,inf) i w (inf) funkcja jest ∪ a nie ∩ jak mi wyszlo

kochanus_niepospolitus: przy pisaniu przedziałów monotoniczności dlaczego nie ozstała uwzględniona dziedzina funkcji

kochanus_niepospolitus: a funkcja jest oczywiście ∩ jeśli chodzi o wklęsłość/wypukłość co wynika chociażby z przedziałów monotoniczności + asymptot w x=−1 i x=1

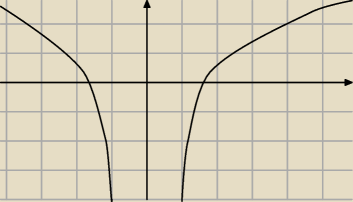
kochanus_niepospolitus: tak pi razy oko

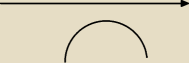
xyz: mimo wszystko dalej nie rozumiem wkleslości , przyblizony wykres mi wyszedl taki

kochanus_niepospolitus: ja narysowałem przybliżony wykres funkcji f(x)

xyz: ale chodzi mi o przyblizony wykres pochodnej drugiego rzędu..

xyz: chodzi mi o sam moment wklęslosci, wg odpowiedzidruga pochodna funkcji powinna być też ∪, mi jednak wychodzi, że cała druga pochodna funkcji jest ∩

xyz: w odp jest blad, juz wiem, dzieki za pomoc^^