Prosze o pomoc Adam: Sprawdzić czy funkcja f(x)=4x³ −5x +14 ma ekstremum dla X=2

karty do gry : Jeśli jej pochodna jest różna od 0 to ekstremum nie ma Jeśli jej pochodna jest równa 0 to : − jeśli druga pochodna jest równa 0 to ekstremum nie ma − jeśli druga pochodna jest różna od 0 to ekstremum jest.

jc: f(x)=x⁴ ma minimum w 0, f'(0)=0, f''(0)=0.

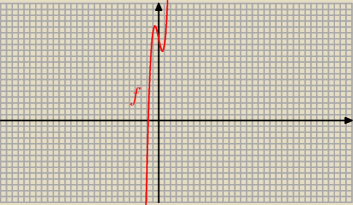
Janek191: f '(x) = 12 x² − 5 f '(2) = > 0 f − nie ma ekstremum w x = 2. Patrz też na wykres funkcji f

karty do gry : Na szczęście mamy tutaj wielomian stopnia III, a nie IV

'Leszek: Wszystkie funkcje postaci f(x) = x^k dla k = 2n , n = N, maja minimum dla x= 0 mimo ze wszystkie pochodne do k−tego rzedu = 0 f_min(0) = 0 , ale f ' (0⁺) > 0 oraz f '(0⁻) < 0

piotr: Jeśli pierwsza z pochodnych nie równych zeru w punkcie x₀ jest rzędu nieparzystego, to funkcja nie ma w punkcie x₀ ani maksimum, ani minimum. Jeśli taką pochodna jest pochodna rzędu parzystego, funkcja ma w punkcie x₀ albo minimum albo maksimum w zależności od tego, czy pochodna ta jest ujemna czy dodatnia.