funkcje Nick: Rozważmy wszystkie funkcje postaci f : {1,2,...,7} → {1,2,3,4}. Ile z nich to funkcje a) rożnowartościowe b) rosnące c) niemalejące d) "na" a) tutaj na pewno odpowiedź to 0 b) też wydaje mi się, że 0 c) proszę o pomoc d) czy to będzie 4!*4³ ?

Adamm:

	4 0		7 0		4 1		7 1		4 2		7 2		4 3		7 3		4 4		7 4
a)		*		+		*		+		*		+		*		+		*

http://www.wolframalpha.com/input/?i=sum+binomial%5B4,+n%5D*binomial%5B7,+n%5D,+n%3D0...4 =330

Adamm: pomyłka

	4 0	7 0		4 1	7 1		4 2	7 2		4 3	7 3		4 4	7 4
a)			+			+			*2!+			*3!+			*4!

http://www.wolframalpha.com/input/?i=sum+binomial%5B4,+n%5D*binomial%5B7,+n%5D*n!,+n%3D0...4 =1961

Adamm:

	4 0	7 0		4 1	7 1		4 2	7 2		4 3	7 3		4 4	7 4
b)			+			+			+			+			=330

jc: a) 0 b) 0

	9 3
c)

	4 3		4 2		4 1
d) 47 −		37 +		27 −

Adamm:

	10 3
w c) nie będzie		?

tak, a), b) będzie jednak 0

Mila: c) Liczba funkcji niemalejących f:{1,2,3,4,5,6,7}→{1,2,3,4} Kombinacje z powtórzeniami:

4+7−1 7		10 7		10 3
	=		=

d) liczba suriekcji: |A|=7, |B|=4

	4 k
∑(k=0 do 4) (−1)k*		*(4−k)7 jak podał jc

jc:

	10 3
Oczywiście, że

= liczba rozwiązań nierówności x₁+x₂+ .. + x₇ ≤ 3 lub liczba rozwiązań równania x₁+x₂+ .. + x₇ + x₈ = 3 (w nieujemnych liczbach całkowitych) f₁=1+x₁ f₂=1+x₁+x₂ f₃=1+x₁+x₂+x₃ ...

Adamm: ja o tym myślałem w ten sposób liczba rozwiązań równania x₁+x₂+x₃+x₄=7 x₁, x₂, x₃, x₄ symbolizują ile razy f przyjmuje wartości 1, 2, 3, 4

jc: Adamm, Twoje spojrzenie mi się bardziej podoba. Zapamiętam. To po prostu liczba dróg na szachownicy o rozmiarach 8x4. Idziemy od lewego dolnego pola do prawego górnego (w prawo lub do góry). Pomijamy 8 kolumnę i mamy wykres naszej funkcji. Ja patrzę z jednej strony, Ty z drugiej.

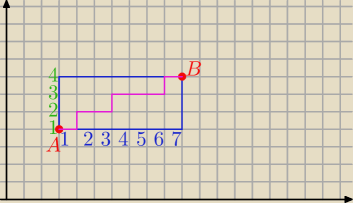
Mila: Przykład funkcji niemalejącej: f(x₁)=1 f(x₂)=2 f(x₃)=2 f(x₄)=3 f(x₅)=3 f(x₆)=3 f(x₇)=4 {1,2,2,3,3,3,4}− ciąg niemalejący o długości 7 o wyrazach ze zbioru B={1,2,3,4}, |B|=4

jc: Mila, właśnie o to mi chodziło. Mamy 7 kroków w prawo i 3 do góry. I zawsze otrzymamy pewien wykres funkcji niemalejącej.

Mila: