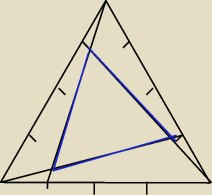
 Każdy bok trójkąta równobocznego dzieli się na cztery równe części. Pole trójkąta wynosi
1001cm2. Oblicz pole trójkąta znajdującego się w środku. (zaznaczonego na niebiesko, załączam
rysunek poglądowy)
Każdy bok trójkąta równobocznego dzieli się na cztery równe części. Pole trójkąta wynosi
1001cm2. Oblicz pole trójkąta znajdującego się w środku. (zaznaczonego na niebiesko, załączam
rysunek poglądowy)
| P | P | 3 | ||||
P = 1001, A = P − 3* | + 3* | = P* | ||||
| 4 | 60 | 10 |
| 3 | ||
mi wyszło że to | oryginalnego pola | |
| 7 |
| 4 | |
P | |
| 13 |


 1/ 3(u+w)=3u+w+S ⇒ S=2w
2/ P=20u+4w i P=3w+12u+S ⇒ w=8u to S=16u
1/ 3(u+w)=3u+w+S ⇒ S=2w
2/ P=20u+4w i P=3w+12u+S ⇒ w=8u to S=16u
| P | ||
3/ P=24u+12u+2w ⇒ P=52u ⇒ u= | ||
| 52 |
| 16P | 4P | |||
4/ S= | = | |||
| 52 | 13 |
| P | ||
Znalazłem swój błąd − zapomniałem o dwójce w równaniu kosinusów i stąd wyszło mi u= | . | |
| 60 |
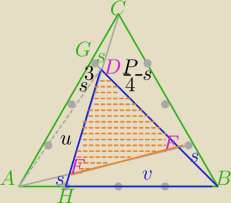
| 3 | P | 1 | ||||
PΔHBD= | P−( | −s)= | P+s | |||
| 4 | 4 | 2 |
| P | ||
PΔAHD=u= | −4s | |
| 4 |
| 1 | P | |||
PΔHBD=3*PΔAHD⇔ | P+s=3*( | −4s)⇔ | ||
| 2 | 4 |
| P | ||
s= | ||
| 52 |
| P | 2P | 11P | ||||
v= | − | = | ||||
| 4 | 52 | 52 |
| P | P | 11P | 4P | 4*1001 | ||||||
PΔDEF= | + | − | = | = | ||||||
| 2 | 52 | 52 | 13 | 13 |