 Ukorzenione, czyli jeden z wierzchołków jest szczególny, wybrany (korzeń) i jego stopień nie
jest większy niż 2 (może być równy 1 czy nawet 0 dla drzewa o 1 wierzchołku).
Oznaczmy przez f(n) liczbę ukorzenionych drzew binarnych o n wierzchołkach (z dokładnością do
izomorfizmu).
f(1)=1
f(2)=f(1)=1 // do korzenia jako gałęzie dokładasz drzewa: (0,1) elementowe
Ukorzenione, czyli jeden z wierzchołków jest szczególny, wybrany (korzeń) i jego stopień nie
jest większy niż 2 (może być równy 1 czy nawet 0 dla drzewa o 1 wierzchołku).
Oznaczmy przez f(n) liczbę ukorzenionych drzew binarnych o n wierzchołkach (z dokładnością do
izomorfizmu).
f(1)=1
f(2)=f(1)=1 // do korzenia jako gałęzie dokładasz drzewa: (0,1) elementowe
| ||||||||
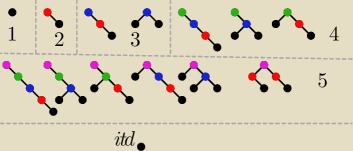
f(3)=f(2)+f(1)+ | =1+1+0=2 // dokładasz drzewa: (0,2), (1,1) elementowe | |||||||
| ||||||||
f(5)=f(4)+f(1)f(3)+f(2)+ | =3+1*2+1+0=6 // (0,4), (1,3), (2,2) | |||||||
| ||||||||
f(7)=f(6)+f(1)f(5)+f(2)f(4)+f(3)+ | =11+1*6+1*3+2+1=23 // (0,6), (1,5), (2,4), (3,3) | |||||||