pochodna Michał: pochodna f(x)=e^4x − 2e^2x f'(x)=4e^3x − 4e^x dobrze to jest?

paziówna: e^4x to złożenie funkcji. więc dla obu składników musisz policzyć jeszcze pochodne wykładników, tzn.: (e^4x)' = 4e^3x*(4x)' analogicznie drugi

Bogdan: Nie

Bogdan: f(x) = a*e^g(x) = a*g'(x)*e^g(x)

Michał: no właśnie czyli 4e^4x − 4e^2x

Piotrek: czyli będzie 4e⁴x

Piotrek: BRAWO MICHAŁ

paziówna: racja, proszę o wybaczenie

Piotrek: A kto zrobi takie: Zbadać monotoniczność i wyznaczyć ekstrema. f(x)= e⁴x − 2e²x Jak już wiemy: f'(x)= 4e⁴x − 4e²x ... tylko co dalej ?

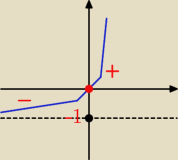
Bogdan: f'(x) = 4e^4x − 4e^2x = 4e^2x(e^2x − 1) Rysunek przedstawia wykres y = e^2x − 1 (linia jest krzywą, a nie łamaną) Dla każdej wartości x: 4e^2x > 0 Pochodna zmienia znak z minus na plus w punkcie x = 0, w tym punkcie funkcja posiada minimum: y_min = f(0) = e⁰ − 2e⁰ = 1 − 2 = −1 Pochodna jest ujemna dla x < 0, w tym przedziale funkcja jest malejąca Pochodna jest dodatnia dla x > 0, w tym przedziale funkcja jest rosnąca.

Piotrek: no dzięki wielkie

Piotrek: A takie samo polecenie dla funkcji f(x)= ln⁴ x − 2 ln² x

niki: e⁴

john2: (e⁴)' = 0