funkcja analityczna. Anka.: Punkty A(2, 2) i B(4, −1) są dwoma kolejnymi wierzchołkami kwadratu ABCD. Wyznacz współrzędne pozostałych wierzchołków tego kwadratu. Pomocy, nic kompletnie nie kumam.

Julek: zauważ, że są to kolejne wierzchołki kwadratu, więc tworzą jeden bok, którego długość obliczysz ze wzroku |AB| = √(x₁−x₂)² + (y₁ − y₂)² długość wynosi √13 teraz chcąc znaleźć trzeci wierzchołek, np. D musisz postawić dwa warunki : − odległość od punktu A do D jest równa √13 − odległość od punktu B do D jest równa tyle co przekątna kwadratu (d= a√2), więc √26 |AD| = √13 |BD| = √26 masz układ z dwiema niewiadomymi : √13 = √(2−x)² + (2−y)² √26 = √(4−x)² + (1+y)² z wierzchołkiem C postępujesz analogicznie Pozdrawiam

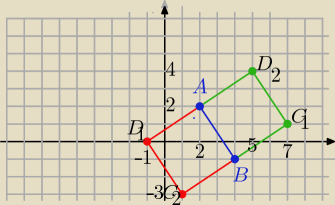
Eta: Podam inne rozwiązanie ( wykorzystując własności wektorów) → ja nie piszę strzałek nad AB ( ale należy je pisać) wektory AB i BC oraz AD i AC są prostopadłe ( i mają równe długości) więc ich iloczyn skalarny = 0 AB=[ 2,−3] CB=[ 4−x_C , −1−y_C] to CB= [ −3,−2] lub BC= [3,2] to: 4−x_C = −3 i −1−y_C= −2 lub 4−x_C= 3 i −1−y_C= 2 x_C= 7 i y_C= 1 => C₁( 7,1) lub x_C = 1 i y_C= −3 => C₂( 1, −3) podobnie DC= [ x_D−2, y_D−2] i AB= [ 2, −3] to: CD=[ −3,−2] lub CD= [ 3,2] x_D−2= −3 i y_D−2= −2 lub x_D−2= 3 i y_D −2= 2 x_D= −1 i y_D= 0 => D₁( −1,0) lub x_D= 5 i y_D= 4 => D₂( 5, 4) tak więc są dwa takie kwadraty spełniające warunki zadania .

Anka.: dziękuje wam za pomoc !

ithem: czy może mi ktoś powiedzieć dlaczego 4−xC = −3 w zapisie AB=[ 2,−3] CB=[ 4−xC , −1−yC] 4−xC = −3 i −1−yC= −2 lub 4−xC= 3 i −1−yC= 2

ithem: dlatego że w iloczynie skalarnym można zamieniać miejscami czy jak?

ithem: poza tym istnieje jakiś błąd w obliczeniach C=(8,1) i C'=(0,−3)

hhh: ≥∞∞

hqfgqg: Julek,jakim cudem ci wyszlo " √13 " .... gdy z równania wychodzi pierwiastek z 15

Eta: A no "takim cudem" → A(2,2) , B(4,−1) AB=[2, −3] to |AB|= √4+9= √13

tyu: cześć, czy ktoś mógłby tutaj pomóc w obliczeniach? Julek i Eta przyjęli, że A(2, 2) i B(4, −1) − tak jak podane w poście, a w zadaniu w zbiorze zadań są współrzędne A(2, 3) i B(4, −1) Ja przyjąłem, że A(2, 3) i B(4, −1), więc IABI= 2√5 zatem IBDI= 2√10 zatem powstaje układ równań IADI 2√5 = √ (x−2)² + (3−y)² IBDI 2√10 = √ (x−4)² + (y+1)² odjąłem to stornami i wychodzi mi x=2y−4 i dalej co mam z tym zrobić. Co do rozwiązania Ety, to nie wiem skąd się wzięło "CB= [ −3,−2] lub BC= [3,2]" − czy to jest ustalone na podstawie rysunku, czy z obliczeń. Bo jeśli z rysunku, to rozumiem, ale jeśli z obliczeń algebraicznych, to jak to obliczyć, bo nie wiem tego.

tyu: czy ktoś pomoże ?

zaqwsx: Eta podała dobry sposób itp wszystko dobrze ale wzieła wektor AB i napisała [2,−3] a w rzeczywistości jest to wektor AB[2,−4] mała pomyłka a tak dużo zmienia. dlatego w książce są inne odpowiedzi niż tutaj, wszystko inne okej.

b.: cóż to za forumowa archeologia wątek odkopany po prawie 5 latach

zaqwsx: wracajac do tego to Anka popełniła bład bo w punkcie A napisała (2,2) nie 2,3

zaqwsx: i tak chciałem objaśnić dla potomnych