Funkcja kwadratowa z parametrem i wartością bezwzględną. Pytajnik: Witam, czy potrafi ktoś rozwiązać to równanie w algebraiczny sposób z wytłumaczeniem? Wyznacz te wartości parametru m(m∊R), dla których równanie x*|x+1|−x=6−2m. (|x+1|) oznacza moduł z x+1 Z góry dziękuję

Jerzy: Jakie jest pytanie ?

Pytajnik: Przepraszam, część mi się wykasowała: Wyznacz te wartości parametru m(m∊R), dla których równanie x*|x+1|−x=6−2m ma więcej rozwiazań ujemnych niz dodatnich. Zalezy mi na rozwiazaniu algebraicznym a nie rysowaniu wykresu.

Omikron: Dlaczego zależy Ci na rozwiązaniu algebraicznym? Zadania w których da się m przerzucić na jedną stronę a x na drugą najłatwiej się robi rysując wykres i odczytując.

Jerzy: Rozpatrujesz oddzielnie dwa przypadki: 1) x + 1 ≥ 0 i wtedy masz równanie: x² + x − x = 6 − 2m 2) x + 1 < 0 i ...................................: −x² − x − x = 6 − 2m

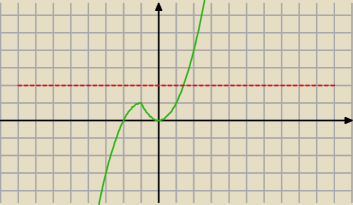
Jerzy: Czerwona prosta: y = 6 − 2m

Pytajnik: Chciałbym zobaczyć rozwiązanie algebraiczne, ponieważ wydaje mi się trudne, nie mogę sobie z tym poradzić, a jestem człowiekiem, który próbuje aż do skutku, więc chciałbym poznać też tąmetoda rozwiązania. Poza tym, chodzi mi też o to, że dla "brzydkich danych" z wykresu ciężko będzie odczytać współrzędne przecięcia wykresów funkcji itd. Czy mogę w takim razie liczyć na rozwiązanie algebraiczne?

Omikron: Niedziwne, że wydaje się trudne, bo tego typu zadanie po prostu rozwiązuje się przy pomocy wykresu. Nie trafisz na zadanie tego typu, w którym nie będzie się dało odczytać punktu przecięcia. Zapewne da się to zrobić algebraicznie, ale będzie to niepotrzebne komplikowanie sobie życia. Trzeba podzielić na dziedziny, żeby zdjąć moduł, w każdej dziedzinie rozwiązać równanie w zależności od delty i określić kiedy jakie znaki będą miały rozwiązania. Następnie trzeba w każdym z przypadków porównywać że sobą dwa równania i sprawdzać czy więcej jest rozwiązań dodatnich czy ujemnych. Moim zdaniem szkoda na to czasu i lepiej narysować wykres.