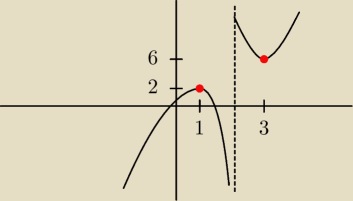
Czy minimum lokalne może być większe od maksimum Konrad: Cześć, tak ja w temacie, Czy minimum lokalne może być większe od maksimum? Treść zadania: Wyznacz ekstrema funkcji f(x) = x²−3/x−2 Miejsca zerowe to 1 i 2, Dziedzina to x∊R / {2}. Wychodzi mi że minimum to (3,6) a maksimum (1,2), ale nie wiem czy poprawnie to zinterpretowałem.

Adamm: minimum lokalne, jest tak jak nazwa wskazuje, lokalne

Konrad: Dzięki, ale pytanie brzmiało, czy minimum lokalne może być większe od maksimum lokalnego (odpowiedź tak lub nie) To że nazwa minimum lokalne wskazuje na jego lokalność, to zauważyłem już jakiś czas temu

Adamm: oczywiście że tak