Monotoniczność funkcji Roman: Panowie mam problem z 3 zadaniami z monotoniczności funkcji. Rozwiązując 2 poradzę sobie z 3. Zacznę od moim zdaniem najprostszego. Zbadaj monotoniczność funkcji: a) y=2x⁵−10x⁴+10x³−2 D=R f'(y) = 10x⁴−40x³+30x² D'=D 10x⁴−40x³+30x²=0 x²(10x²−40x+30)=0 x²=0 x₁=0 x₂ = 0 (0 występuje dwukrotnie, więc wykres się będzie odbijał od 0) 10x²−40x+30=0|:10 x²−4x+3=0 Δ=4

	4−2
x1 =		=1
	2

	6
x2=		=3
	2

↗(−∞,0)u(0;1)u(3;+∞) ↘(1;3) zaś odp. w książce jest następująca: ↗(−∞,1)u(3;+∞) ↘(1;3) Kolejne zadanie z logarytmami y=xlnx Df = x>0

	x
f'(y)= (x)'lnx+x(lnx)=lnx+		=lnx+1
	x

D'f = Df lnx+1=0)|e^(...) x+e=1 x=1−e

Jerzy: Ad 1) Zauważ, jak się zmienia znak pochodnej w x = 1 oraz x = 3

Jerzy: Zad 2) Źle policzone miejsce zerowe pochodnej

'Leszek: W drugim zadaniu masz blad : ln x +1 =0 ⇔ ln x = −1 ⇒ x = e⁻¹

Jerzy: I jeszcze jedna uwaga...argumentem pochodnej jest x, a nie y: f'(x) , a nie f'(y) !

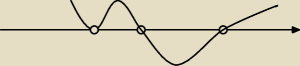
Roman: taki wykres byłby wg mnie − nie wiem dlaczego 0 nie jest brane pod uwagę na wykresie. Możesz nieco dosadniej przedstawić Jerzy swój punkt widzenia.

Roman: Zadanie 2 więc rozwiązane, dzięki @ Jerzy i @'Leszek

Jerzy: Patrz na swój wykres... Dla x < 1 pochodna jest dodatnia, funkcja rośnie Dla x ∊ (1;3) pochodna jest ujemna , funkcja maleje Dla x > 3 , pochodnia jest dodatnia funkcja rośnie.

Roman: już wiem, ponieważ jest to suma przedziałów. Dzięki Jerzy. Pozdrawiam

jc: A na jakim przedziale funkcja f(x)=x² jest rosnąca? Bo podejrzewam, że wg tego podręcznika funkcja rośnie dla x>0, a przecież rośnie dla x≥0.