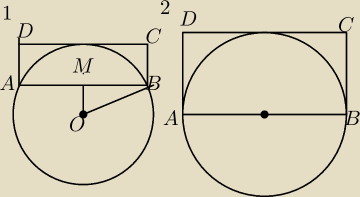
 dany jest okrag o promieniu r i taki prostokat ABCD ze A i B naleza do okregu , bok zas CD
jest do tego okregu styczny
a) Oblicz boki tego prostokata wiedzac z ejego obwod jest rowny 6r
b) Oblicz boki prostokata wiedzac z e jego obwod wynosi 4r
c) znajdz najwieksza wartosc k dla ktorej zadanie ma rozwiazanie i obwo prostokata jest rowny
kr.
Oblicz dlugosci bokow prostokata dla tej wartosi k . Wykonaj odpowiednie rysunki
Mam tutaj narysowane dwa przypadki i w osobnym poscie narysuje trzeci
dany jest okrag o promieniu r i taki prostokat ABCD ze A i B naleza do okregu , bok zas CD
jest do tego okregu styczny
a) Oblicz boki tego prostokata wiedzac z ejego obwod jest rowny 6r
b) Oblicz boki prostokata wiedzac z e jego obwod wynosi 4r
c) znajdz najwieksza wartosc k dla ktorej zadanie ma rozwiazanie i obwo prostokata jest rowny
kr.
Oblicz dlugosci bokow prostokata dla tej wartosi k . Wykonaj odpowiednie rysunki
Mam tutaj narysowane dwa przypadki i w osobnym poscie narysuje trzeci
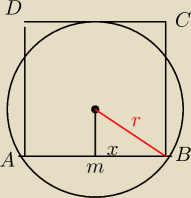 Oznaczam sobie AB= CD=2x
BC= AD= y
Napewno dla kazdego przypadku bedzieli mieli ze
x≤r i y<2r i k>0
oraz (y−r)2+x2= r2
mam tylko wskazowke do zadania
Oznaczam sobie AB= CD=2x
BC= AD= y
Napewno dla kazdego przypadku bedzieli mieli ze
x≤r i y<2r i k>0
oraz (y−r)2+x2= r2
mam tylko wskazowke do zadania
| k | ||
AB+BC= | *r | |
| 2 |
| k | ||
Jesli k−−− to obwod to to | to polowa obwodu i sie zgadza . Ale po co tam jest to r? | |
| 2 |
| 4 | ||
więc gdy x = 0 (czyli prawy rysunek) lub x = − | (czyli M jest 'poniżej' środku | |
| 5 |
 Bardziej chodzilo mi o to r ale juz doszlem dlaczego .
W warunku zadania mam 6r i 4r .
Po wyjezdzie zajme sie tym dalej .
Bardziej chodzilo mi o to r ale juz doszlem dlaczego .
W warunku zadania mam 6r i 4r .
Po wyjezdzie zajme sie tym dalej .
| +/−r*√−k2+4k+16 − kr + 2r | ||
2(r−x) + 4√r2−x2 = kr ⇒ x = | ||
| 10 |
| 1 | ||
{2x+y= | k*r | |
| 2 |
| kr−2y | ||
zdrugiego wyznaczylem x = | ||
| 4 |
| kr−2y | ||
(y−r)2+( | )2= r2 | |
| 4 |
| 3r−y | ||
mam 5Y6−14ry+9r2=0 i x= | ||
| 2 |
| 9 | 3 | |||
y2= | ri x2= | r | ||
| 5 | 5 |
| 6 | 9 | |||
lub AB= CD= | r i BC=AD= | r | ||
| 5 | 5 |
| 2r−y | ||
5y2−12ry+4r2=0 i x= | ||
| 2 |
| 2 | 4 | |||
U{y1= | r i x1= | r | ||
| 5 | 5 |
| 8 | 2 | |||
To AB=CD= | r i BC=AD= | r | ||
| 5 | 5 |
| 4√5r | ||
wtedy AB= Cd= | ||
| 5 |
| r(5+√5 | ||
BC= AD= | ||
| 5 |

 na razie dosc bo do pracy niedlugo trza jechac
na razie dosc bo do pracy niedlugo trza jechac