Na ile sposobów można posadzić ludzi przy okrągłym stole. Pytanie-d: Przy okrągłym stole losowo posadzono 2x Niemców, 2 x Włochów i 2x Polaków. Na ile sposób możemy ich posadzić tak by osoby tej samej narodowości nie siedziały kolo siebie .

Pytający: Rozróżniamy Światowida od Dobromira czy Polak to Polak?

Pytanie-d: dwie osoby tej samej narodowości są nierozróżnialne

Mila: 24?

Pytający: Wg mnie 5 sposobów (zakładając, że miejsca przy stole są nierozróżnialne): 1. Jeden Polak sąsiaduje z Niemcami, drugi z Włochami. P N N W W P 2. Polacy mają po lewej Włocha, po prawej Niemca. P N W W N P 3. Polacy mają po lewej Niemca, po prawej Włocha. P W N N W P 4. Jeden Włoch sąsiaduje z Niemcami, drugi z Polakami. P N W W N P 5. Jeden Niemiec sąsiaduje z Włochami, drugi z Polakami. P W N N W P

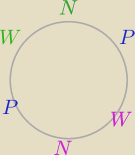
Mila: Witaj. Tak myślałam, (może z nadmiarem?) npw mogę ustawić na 3! =6 sposobów Jeden z przypadków : posadzę: npwnpw dwa środkowe mogę między sobą przestawić, dwa zewnętrzne też.

jc: 192 ?

Mila: Jak liczyłeś jc ? Jaka teoria?

Adamm: według mnie jest 8 sposobów

Adamm: cofam to popieram Pytającego

jc: Mamy 4 schematy ABACAC ABCACB ABCABC ABCBAC Pod A,B,C podstawiamy P,N,W (za każdym razem 6 sposobów) Potem możemy jeszcze zamieniać ludzi w parach (8 sposobów). Razem 4*6*8=192.

jc: W pierwszym powinno być ABACBC.

Pytający: Witaj, Milu. Nie przyszedł mi właśnie do głowy prosty sposób na policzenie tego, wydaje mi się, że mój sposób jest prosty: sadzamy 2 Polaków naprzeciwko i albo sadzamy pomiędzy nich po 2 osoby (pierwsze 3 przypadki), albo odpowiednio 1 i 3 osoby (kolejne 2 przypadki). Innych możliwości nie widzę. Jeśli dobrze rozumiem Twój zapis: owszem, możesz przestawić dwa środkowe czy dwa zewnętrzne, ale jedno przestawienie uniemożliwia kolejne (ze względu na niemożność sąsiadowania rodaków). Można by spróbować policzyć to w ten sposób: jedną osobę usadzamy, pozostałe dosadzamy na

	5!
(6−1)! sposobów, ale 3 par osób nie rozróżniamy, więc różnych usadzeń jest		=15.
	2!*2!*2!

Należy wyeliminować przypadki, gdy jacyś rodacy ze sobą sąsiadują.

Pytający: jc, np. te schematy są takie same (zamienione litery i cyklicznie preszunięte): ABCACB ABCBAC

Mila: Witaj Pytający, coś mi się plącze w głowie, że już kiedyś to rozwiązałam , ale cóż skleroza. Pozdrawiam wszystkich. Szkoda, że autor nie współpracuje, może ma odpowiedź, albo poda przy jakiej teorii to jest podane.

Mila: ABCABC ACBACB BACBAC BCABCA CABCAB CBACBA i możliwe przestawienia.

Mila: DOBRANOC

jc: U mnie to 2 różne schematy. Jeśli nie rozróżniamy osób tej samej narodowości to mamy 24 sposoby. Ale o tym było dopiero w kolejnych wpisach.

Pytanie-d: Nie mam rozwiązania do tego zadania to zadanie zadane przez wykładowce, pogubiłem się w waszych rozwiązaniach, które jest najbardziej prawdopodobne? Dodam, że stół nie ma ponumerowanych miejsc można go dowolnie obrać a zdarzenia są identyczne. Wgl co dzieje się w przypadku gdy dwóch polaków jest rozróżnialnych i zdarzenia N1P1W1N2P2W2 i N1P2W1N2P1W2 są różne ile wtedy może być sposóbów

Pytający: Obstaję przy mojej odpowiedzi, tj 5 sposobów. Jeśli zaś rozróżniamy osoby tej samej narodowości, łącznie mamy (6−1)!=120 różnych ustawień przy stole (usadzamy jedną osobę, a pozostałe 5 permutujemy na pozostałych miejscach). Oznaczmy: S(P) − liczba ustawień, w których Polacy ze sobą sąsiadują S(P∩N) − liczba ustawień, w których Polacy ze sobą sąsiadują i Niemcy również ze sobą sąsiadują itd. Wtedy z zasady włączeń i wyłączeń, liczba ustawień takich, że rodacy nie sąsiadują wynosi: 120−(S(P)+S(N)+S(W)−S(P∩N)−S(P∩W)−S(W∩N)+S(P∩N∩W))= =120−(2*4!+4*2*3!+4*2*3!−2*3*2*2−2*3*2*2−3*2*2*2+2*2*2*2)=32 Jak to było liczone? Ustawiamy np. jednego Polaka na stałym miejscu: P1xxxxx I wtedy: − S(P): Polacy muszą sąsiadować, więc mamy 2 sposoby na dosadzenie P2: P1P2xxxx lub P1xxxxP2 na pozostałych miejscach sadzamy pozostałych na 4! sposobów, zatem S(P)=2*4!. − S(W∩N): Niemcy i Włosi muszą sąsiadować, więc ustawienie musi wyglądać: P1AABBx lub P1AAxBB lub P1xAABB Mamy 3 schematy, dla każdego wybieramy czy A to Niemcy czy Włosi oraz Niemców możemy zamienić kolejnością i Włochów również, w miejsce x sadzamy P2 na 1! sposobów, zatem S(W∩N)=3*2*2*2. − pozostałe przypadki rozpatrujemy analogicznie

jc: Jeśli nie odróżniasz jednego Polaka od drugiego, itd. oraz utożsamiasz sytuacje uzyskane przez obrót, to faktycznie masz 5 możliwości. Ale ani o jednym ani o drugim w treści zadania mowy nie było.

kochanus_niepospolitus: Jak dla mnie to treść zadania jest niedoprecyzowana, jak zresztą 'jc' napisał. Nie ma podanego czy ludzie danej narodowości są rozróżnialni (a przeważnie są ) oraz czy miejsca przy stole są rozróżnialne. Gdybyśmy mieli tutaj liczyć prawdopodobieństwo, to problemu by nie było ... ale tak nie jest.