Na rysunku przedstawiony jest wykres funkcji homograficznej F(x) = Piotr:

	ax + 1
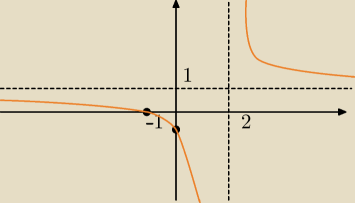
Na rysunku przedstawiony jest wykres funkcji homograficznej F(x) =		, gdzie x≠
	cx + d

	d
−		i ad − c ≠ 0. Korzystając z rysunku oraz wiedząc,że miejscem zerowym funkcji F jest
	c

	1
liczba −1, zaś wykres funkcji F ma z osią OY punkt wspólny (0, −		), wyznacz wartości
	2

współczynników a, c, d. Następnie rozwiąż równanie F(x) + 0,5 * (x − 1)² = 2.

	a
Proszę o pomoc! Wiem ze muszę podstawić do wzoru f(x)=		+q ale co dalej....
	x−p

Piotr:

	x−1
Dobra, nie wiem czy dobrze ale wyszło mi		. Z czego wynika że a=1, c=1, d=−2. Pomoże
	x−2

ktoś rozwiazać równanie?

powrócony z otchłani: Jak aci pomglo w liczniku wyjsc x−1

powrócony z otchłani:

	x+1
Winno wyjsc
	x−2