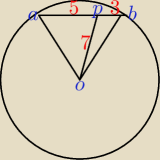
PLANIMETRIA nahh: W kole o środku O poprowadzono cięciwę AB. Punkt P dzieli te cieciwe na odcinki o długościac 5 i 3, jak na rysunku obok. Odcinek OP ma długość 7. Oblicz promień koła i pole wycinka koła wyznaczonego przez kąt AOB.

Milo: Niech kąt APO=α Wówczas ką BPO=180−α |AO|=|BO|=r Z twierdzenia cosinusów: 5²+7²−2*5*7*cosα=r² 3²+7²+2*3*7*cosα=r² (bo cos(180−α)=−cosα) 74−70cosα=r²

	70
58+42cosα=r2 /*
	42

	2		70
96		+ 70cosα =		r2
	3		42

Po dodaniu stronami:

	2		112		42
170		=		r2 /*
	3		42		112

r²=64 r=8 Sprawdź obliczenia, mogłem się gdzieś pomylić

Janek191: r² = 49 + 25 − 2*7*5 cos α = 74 − 70 cos α r² = 49 + 9 − 2*7*3 cos (180^o − α) = 58 + 42 cos α więc 74 − 70 cos α = 58 + 42 cos α 112 cos α = 16

	16		1
cos α =		=
	112		7

oraz

	1
r2 = 74 − 70*		= 64
	7

r = 8 ==== Kąt środkowy β = 60^o więc

	1
Pw =		π r2 =
	6