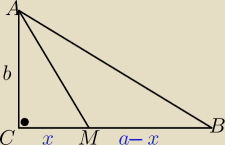
kwadratowa 5-latek: W trojkacie ABC kąt C =90^o AC=b, BC=a M∊BC MB jest srednia arytmetyczna AM i MC . Oblicz MC. Podaj warunki rozwiazalnosci zadania ,oraz liczbe rozwiazan Zalozenie a>0 i b>0 tak mysle ze AM= √b²+x² i x>0

	AM+CM
BM=
	2

	AM+x
a−x=
	2

2(a−x)= AM+x AM+x= 2(a−x) AM+x= 2a−2x AM= 2a−3x Porownujac AM dostaje √b²+x²= 2a−3x ale tez x>0

	2
2a−3x≥0 ⇒x<		a
	3

Podnosze do potegi drugiej b²+x²= 4a²−12ax+9x² −8x²+12ax−4a²+b² =0 ⇒ 8x²−12ax+4a²−b²=0 Δ= B²−4ac Δ= 144a²−4*8(4a²−b²) Δ= 144a²−128a²+32b² Δ= 16a²+32b² Δ= a²+2b²

	12a−√a2+2b2
x1=
	16

Tutaj sie zatrzymam bo w odpowiedzi mam ze x= U{3a−√a²+2b²{4} ====================

	a−b		a		b
nawet z ebym skorzystal ze wzoru		=		−		to dostane x1=
	c		c		c

	12a
		−√a2+2b2}{16}=
	16

	3a		√a2+2b2
=		−
	4		16

5-latek: Poprawie W odpowiedzi mam

	3a−√a2+b2
x1=
	4

jc: Dobrze policzyłeś.

5-latek: Witaj dzieki

5-latek:

	12a−√a2+2b2
To tak x1=
	16

	12a+√a2+2b2
a x2=
	16

	2
Ale dla x1 i x2 jest x∊(0,		a) Teraz muszse sprawdzic warunki rozwaizalnosci
	3

czy mam sprawdzic ze x₁>0 i x₂>0 ?

5-latek:

5-latek: Podbijam