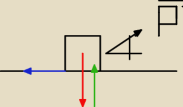
 Ciało o ciężarze Q znajduje się na poziomej płaszczyźnie. Współczynnik tarcia wynosi μ. Jaki
musi być kąt
nachylenia β linii działania siły P i jaka będzie wartość tej siły jeśli przesuwanie się ciała
ma nastąpić przy najmniejszej wartości siły P?
Rysunek wygląda mniej więcej tak :
niebieska linia − siła tarcia
czerwona linia−ciężar ciała Q
zielona linia−siła nacisku
czarna linia−siła P pod kątem β
wiem ,że coś trzeba pokombinować z pochodną , tylko pytanie co ?
Ciało o ciężarze Q znajduje się na poziomej płaszczyźnie. Współczynnik tarcia wynosi μ. Jaki
musi być kąt
nachylenia β linii działania siły P i jaka będzie wartość tej siły jeśli przesuwanie się ciała
ma nastąpić przy najmniejszej wartości siły P?
Rysunek wygląda mniej więcej tak :
niebieska linia − siła tarcia
czerwona linia−ciężar ciała Q
zielona linia−siła nacisku
czarna linia−siła P pod kątem β
wiem ,że coś trzeba pokombinować z pochodną , tylko pytanie co ?
| Qμ | ||
P* cos β = μ ( Q − P sin β)⇒ P = | ||
| cos β + μ sin β |
| −Qμ ( − sin β +μ cos β) | ||
P ' = | ||
| ( cos β + μ sin β )2 |